Câu hỏi:
15/05/2023 1,950
Cho ∆ABC vuông tại A, đường cao AH. Gọi HD, HE lần lượt là đường cao của ∆AHB và ∆AHC. Chứng minh rằng:
a) \(\frac{{A{B^2}}}{{A{C^2}}} = \frac{{HB}}{{HC}}\).
b) \(\frac{{A{B^3}}}{{A{C^3}}} = \frac{{BD}}{{EC}}\).
Cho ∆ABC vuông tại A, đường cao AH. Gọi HD, HE lần lượt là đường cao của ∆AHB và ∆AHC. Chứng minh rằng:
a) \(\frac{{A{B^2}}}{{A{C^2}}} = \frac{{HB}}{{HC}}\).
b) \(\frac{{A{B^3}}}{{A{C^3}}} = \frac{{BD}}{{EC}}\).
Câu hỏi trong đề:
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải:
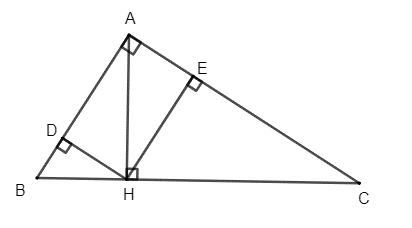
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được: \(\left\{ {\begin{array}{*{20}{c}}{A{B^2} = BH.BC}\\{A{C^2} = CH.BC}\end{array}} \right.\)
\( \Rightarrow \frac{{A{B^2}}}{{A{C^2}}} = \frac{{BH.BC}}{{CH.BC}} = \frac{{HB}}{{HC}}\). (đpcm)
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HD là đường cao ứng với cạnh huyền AB, ta được:
\(BD.BA = B{H^2} \Leftrightarrow BD = \frac{{H{B^2}}}{{AB}}\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:
\(CE.CA = C{H^2} \Leftrightarrow EC = \frac{{H{C^2}}}{{AC}}\)
Ta có: \(\frac{{BD}}{{EC}} = \frac{{H{B^2}}}{{A{B^2}}}:\frac{{H{C^2}}}{{AC}}\)
\( \Leftrightarrow \frac{{BD}}{{EC}} = \frac{{H{B^2}}}{{AB}}.\frac{{AC}}{{H{C^2}}}\)
\( \Leftrightarrow \frac{{BD}}{{EC}} = {\left( {\frac{{HB}}{{HC}}} \right)^2}.\frac{{AC}}{{AB}}\)
\( \Leftrightarrow \frac{{BD}}{{EC}} = {\left( {\frac{{A{B^2}}}{{A{C^2}}}} \right)^2}.\frac{{AC}}{{AB}}\)
\( \Leftrightarrow \frac{{BD}}{{EC}} = {\left( {\frac{{AB}}{{AC}}} \right)^4}.\frac{{AC}}{{AB}}\)
\( \Leftrightarrow \frac{{BD}}{{EC}} = \frac{{A{B^4}}}{{A{C^4}}}.\frac{{AC}}{{AB}}\)
\( \Leftrightarrow \frac{{BD}}{{EC}} = \frac{{A{B^3}}}{{A{C^3}}}\). (đpcm)
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho 2 tập hợp \(M = \left[ {2m - 1;2m + 5} \right]\) và \(N = \left[ {m + 1;m + 7} \right]\)(với m là tham số thực). Tính tổng tất cả các giá trị của m để hợp của 2 tập hợp M và N là 1 đoạn có độ dài bằng 10.
Xem đáp án »
15/05/2023
17,474
Câu 2:
Một hồ bơi dạng hình hộp chữ nhật có kích thước trong lòng hồ là: Chiều dài 12m, chiều rộng 5m, chiều sâu 3m.
a. Tính thể tích của hồ bơi.
b. Tính diện tích cần lát gạch bên trong lòng hồ (mặt đáy và 4 mặt xung quanh).
c. Biết gạch hình vuông dùng để lát hồ bơi có cạnh 50cm. Hỏi cần mua ít nhất bao nhiêu viên gạch để lát bên trong hồ bơi.
Một hồ bơi dạng hình hộp chữ nhật có kích thước trong lòng hồ là: Chiều dài 12m, chiều rộng 5m, chiều sâu 3m.
a. Tính thể tích của hồ bơi.
b. Tính diện tích cần lát gạch bên trong lòng hồ (mặt đáy và 4 mặt xung quanh).
c. Biết gạch hình vuông dùng để lát hồ bơi có cạnh 50cm. Hỏi cần mua ít nhất bao nhiêu viên gạch để lát bên trong hồ bơi.
Xem đáp án »
12/07/2024
15,454
Câu 3:
Các cột điện trước đây cách nhau 60 m, hiện nay trồng lại cách nhau 45 m. Hỏi sau cột đầu tiên không phải trồng lại thì cột gần nhất không phải trồng lại là cột thứ mấy?
Xem đáp án »
15/05/2023
4,305
Câu 4:
Hai đội công nhân cùng làm một đoạn đường trong 24 ngày thì xong. Mỗi ngày đội thứ hai làm được khối lượng công việc nhiều gấp đôi đội thứ nhất. Hỏi nếu làm một mình thì mỗi đội làm xong đoạn đường đó trong bao lâu?
Xem đáp án »
15/05/2023
3,374
Câu 5:
Cho 3 số dương x, y, z thỏa mãn điều kiện: xy + yz +zx = 1. Tính:
\(A = x\sqrt {\frac{{\left( {{y^2} + 1} \right)\left( {{z^2} + 1} \right)}}{{{x^2} + 1}}} + y\sqrt {\frac{{\left( {1 + {z^2}} \right)\left( {1 + {x^2}} \right)}}{{1 + {y^2}}}} + z\sqrt {\frac{{\left( {1 + {x^2}} \right)\left( {1 + {y^2}} \right)}}{{1 + {z^2}}}} \).
Cho 3 số dương x, y, z thỏa mãn điều kiện: xy + yz +zx = 1. Tính:
\(A = x\sqrt {\frac{{\left( {{y^2} + 1} \right)\left( {{z^2} + 1} \right)}}{{{x^2} + 1}}} + y\sqrt {\frac{{\left( {1 + {z^2}} \right)\left( {1 + {x^2}} \right)}}{{1 + {y^2}}}} + z\sqrt {\frac{{\left( {1 + {x^2}} \right)\left( {1 + {y^2}} \right)}}{{1 + {z^2}}}} \).
Xem đáp án »
15/05/2023
3,123
Câu 6:
Cho hình tròn tâm O, đường kính AB = 8 cm.
a. Tính chu vi hình tròn tâm O đường kính AB, hình tròn tâm M, đường kính AO và hình tròn tâm N, đường kính OB.
b. So sánh tổng chu vi của hình tròn tâm M và hình tròn tâm N với chu vi hình tròn tâm O.
c. Tính diện tích phần đã tô đậm của hình tròn tâm O.
Cho hình tròn tâm O, đường kính AB = 8 cm.
a. Tính chu vi hình tròn tâm O đường kính AB, hình tròn tâm M, đường kính AO và hình tròn tâm N, đường kính OB.
b. So sánh tổng chu vi của hình tròn tâm M và hình tròn tâm N với chu vi hình tròn tâm O.
c. Tính diện tích phần đã tô đậm của hình tròn tâm O.
Xem đáp án »
15/05/2023
2,824
về câu hỏi!