Câu hỏi:
16/05/2023 243
Từ một điểm A nằm ngoài đường tròn (O; R) vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là tiếp điểm). Trên cung nhỏ BC lấy một điểm M bất kỳ, vẽ MI vuông góc với AB, MK vuông góc với AC (I thuộc AB, K thuộc AC).
a) Chứng minh AIMK, ABOC là các tứ giác nội tiếp;
b) Vẽ MP vuông góc với BC (P thuộc BC). Chứng minh \(\widehat {MPK} = \widehat {MBC}\);
c) Chứng minh MI.MK = MP2;
d) Xác định vị trí của điểm M trên cung nhỏ BC để tích MI.MK.MP đạt giá trị lớn nhất.
Từ một điểm A nằm ngoài đường tròn (O; R) vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là tiếp điểm). Trên cung nhỏ BC lấy một điểm M bất kỳ, vẽ MI vuông góc với AB, MK vuông góc với AC (I thuộc AB, K thuộc AC).
a) Chứng minh AIMK, ABOC là các tứ giác nội tiếp;
b) Vẽ MP vuông góc với BC (P thuộc BC). Chứng minh \(\widehat {MPK} = \widehat {MBC}\);
c) Chứng minh MI.MK = MP2;
d) Xác định vị trí của điểm M trên cung nhỏ BC để tích MI.MK.MP đạt giá trị lớn nhất.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
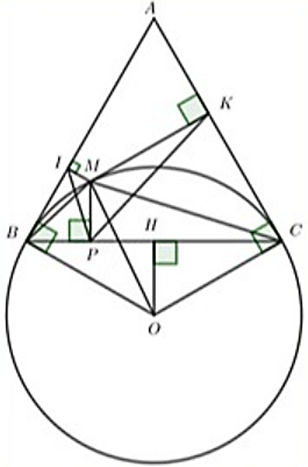
a) Ta có: \(\left\{ \begin{array}{l}MI \bot AB\;\;\;\,\left( {gt} \right)\\MK \bot AC\;\;\left( {gt} \right)\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\widehat {AIM} = 90^\circ \\\widehat {AKM} = 90^\circ \end{array} \right.\)
Tứ giác AIMK có: \(\widehat {AIM} + \widehat {AKM} = 90^\circ + 90^\circ = 180^\circ \)
Þ AIMK nội tiếp đường tròn đường kính AM (đpcm)
Xét (O) có AB, AC là hai tiếp tuyến cắt nhau tại A.
Þ OB ^ AB; OC ^ AC \( \Rightarrow \widehat {ABO} = \widehat {ACO} = 90^\circ \)
Xét tứ giác ABOC có:
\(\widehat {ABO} + \widehat {ACO} = 90^\circ + 90^\circ = 180^\circ \)
Mà hai góc ở vị trí đối nhau
Suy ra tứ giác ABOC nội tiếp.
b) Ta có: MP ^ BC (gt) \( \Rightarrow \widehat {MPC} = 90^\circ \)
MK ^ AC (gt) \( \Rightarrow \widehat {MKC} = 90^\circ \)
\( \Rightarrow \widehat {MPC} + \widehat {MKC} = 90^\circ + 90^\circ = 180^\circ \)
Þ CPMK nội tiếp đường tròn.
\( \Rightarrow \widehat {MPK} = \widehat {MCK}\) (hai góc nội tiếp cùng chắn cung MK)
Mặt khác \(\widehat {MCK} = \widehat {MBC}\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung MC)
\( \Rightarrow \widehat {MPK} = \widehat {MBC}\;\left( { = \widehat {MCK}} \right)\) (đpcm)
c) Ta có:
\(\widehat {MIB} + \widehat {MPB} = 90^\circ + 90^\circ = 180^\circ \)
Þ BPMI là tứ giác nội tiếp
\( \Rightarrow \widehat {MIP} = \widehat {MBC}\) (hai góc nội tiếp cùng chắn cung MP)
Mà \(\widehat {MPK} = \widehat {MBC}\) (cmt)
\( \Rightarrow \widehat {MPK} = \widehat {MIP}\;\left( { = \widehat {MBC}} \right)\)
Tương tự, ta cũng chứng minh được \(\widehat {MPI} = \widehat {MKP}\;\left( { = \widehat {MCB} = \widehat {MBI}} \right)\)
Xét ∆MIP và ∆MPK có:
\(\widehat {MPI} = \widehat {MKP}\) (cmt)
\(\widehat {MIP} = \widehat {MPK}\) (cmt)
Þ ∆MIP ᔕ ∆MPK (g.g)
\( \Rightarrow \frac{{MI}}{{MP}} = \frac{{MP}}{{MK}} \Rightarrow MI.MK = M{P^2}\) (đpcm)
d) Ta có: \(MI.MK = M{P^2}\)
\( \Rightarrow MI.MK.MP = M{P^3}\)
Để tích MI.MK.MP đạt GTLN Û MP đạt GTLN
Gọi H là hình chiếu của O lên BC Þ OH là hằng số (do BC cố định)
Gọi MO Ç BC = {D}
Ta có: MP £ MD; OH £ OD
Þ MP + OH £ MD + OD = MO
Þ MP + OH £ R
Þ MP £ R − OH
Þ MP lớn nhất bằng R − OH
Û O, H, M thẳng hàng hay M bằm chính giữa cung nhỏ BC
Vậy khi M nằm chính giữa cung nhỏ BC thì tích MI.MK.MP đạt GTLN.
Sách thầy cô Vietjack biên soạn
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Tìm tất cả các số tự nhiên n thõa mãn 5n + 14 chia hết cho n + 2.
Xem đáp án »
16/05/2023
13,410
Câu 2:
Tính: \(\frac{1}{3} + \frac{1}{9} + \frac{1}{{27}} + \frac{1}{{81}} + \frac{1}{{243}} + \frac{1}{{729}}\).
Tính: \(\frac{1}{3} + \frac{1}{9} + \frac{1}{{27}} + \frac{1}{{81}} + \frac{1}{{243}} + \frac{1}{{729}}\).
Xem đáp án »
16/05/2023
8,905
Câu 3:
Chứng tỏ rằng: 2x + 3y chia hết cho 17 thì 9x + 5y chia hết cho 17.
Chứng tỏ rằng: 2x + 3y chia hết cho 17 thì 9x + 5y chia hết cho 17.
Xem đáp án »
16/05/2023
7,108
Câu 5:
Cho một số tự nhiên có hai chữ số, biết rằng nếu viết thêm số 64 vào bên trái số đó thì được một số gấp 81 lần số đã cho.
Cho một số tự nhiên có hai chữ số, biết rằng nếu viết thêm số 64 vào bên trái số đó thì được một số gấp 81 lần số đã cho.
Xem đáp án »
16/05/2023
4,838
Câu 7:
Cho góc nhọn a, biết sin a = 0,6. Không tính số đo góc a, hãy tính cos a, tan a, cot a.
Cho góc nhọn a, biết sin a = 0,6. Không tính số đo góc a, hãy tính cos a, tan a, cot a.
Xem đáp án »
16/05/2023
3,324
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
80 câu Bài tập Hình học Khối đa diện có lời giải chi tiết (P1)
-
148 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu từ đề thi Đại học có lời giải (P1)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
-
62 câu Trắc nghiệm Khái niệm về khối đa diện (nhận biết)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận