Câu hỏi:
11/07/2024 479
Cho hai đường thẳng: y = x + 3 (d1); y = 3x + 7 (d2).
a) Gọi A và B lần lượt là giao điểm của (d1) và (d2) với trục Oy. Tìm tọa độ trung điểm I của đoạn thẳng AB.
b) Gọi J là giao điểm của (d1) và (d2) . Tam giác OIJ là tam giác gì? Tính diện tích của tam giác đó.
Cho hai đường thẳng: y = x + 3 (d1); y = 3x + 7 (d2).
a) Gọi A và B lần lượt là giao điểm của (d1) và (d2) với trục Oy. Tìm tọa độ trung điểm I của đoạn thẳng AB.
b) Gọi J là giao điểm của (d1) và (d2) . Tam giác OIJ là tam giác gì? Tính diện tích của tam giác đó.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Vì A là giao điểm của (d1) và Oy nên \(\left\{ \begin{array}{l}{x_A} = 0\\{y_A} = 0 + 3 = 3\end{array} \right.\)
Suy ra A(0; 3).
Vì B là giao điểm của (d2) và Oy nên \(\left\{ \begin{array}{l}{x_B} = 0\\{y_B} = 3.0 + 7 = 7\end{array} \right.\)
Suy ra B(0; 7).
Vì I là trung điểm của AB nên tọa độ của I là
\(\left\{ \begin{array}{l}{x_I} = \frac{{{x_A} + {x_B}}}{2}\\{y_B} = \frac{{{y_A} + {y_B}}}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_I} = \frac{{0 + 0}}{2} = 0\\{y_B} = \frac{{3 + 7}}{2} = 5\end{array} \right.\)
Vậy I(0; 5).
b) Ta có I(0; 5) suy ra OI = 5.
Hoành độ giao điểm của (d1) và (d2) là nghiệm của phương trình:
x + 3 = 3x + 7
⇔ x – 3x = 7 – 3
⇔ – 2x = 4
⇔ x = – 2
Suy ra y = – 2 + 3 = 1
Do đó J(– 2; 1), suy ra \[OJ = \sqrt {{{\left( { - 2} \right)}^2} + {1^2}} = \sqrt 5 \].
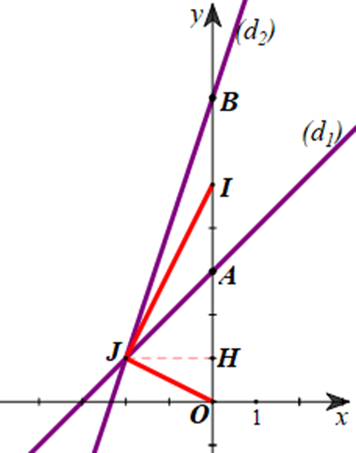
Gọi H là hình chiếu của J lên Oy. Do đó H(0; 1).
Suy ra OH = 1 và JH = 2.
Do đó IH = OI – OH = 5 – 1 = 4.
Khi đó, theo định lí Pythagore ta có: IJ2 = IH2 + JH2
\[ \Rightarrow IJ = \sqrt {I{H^2} + J{H^2}} = \sqrt {{4^2} + {2^2}} = 2\sqrt 5 \]
Suy ra OI2 = OJ2 + JI2
Do đó tam giác OIJ vuông tại J (định lý Pytago đảo)
Ta có \[{{\rm{S}}_{{\rm{OIJ}}}} = \frac{1}{2}JI.J{\rm{O}} = \frac{1}{2}.2\sqrt 5 .\sqrt 5 = 5\]
Vậy tam giác OIJ vuông tại J có diện tích bằng 5.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới)
Đã bán 1,5k
₫ 70.000
₫ 36.000
Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn)
Đã bán 1,4k
₫ 280.000
₫ 150.000
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Hình lập phương có diện tích toàn phần là 54 cm2 . Tính thể tích hình đó.
Hình lập phương có diện tích toàn phần là 54 cm2 . Tính thể tích hình đó.
Xem đáp án »
12/07/2024
6,896
Câu 2:
Giáo viên chủ nhiệm muốn chia 128 quyền vở; 48 bút chì và 192 tập giấy thành một số phần thưởng như nhau cho các học sinh giỏi nhân dịp tổng kết năm học. Hỏi có thể chia nhiều nhất là bao nhiêu phần thưởng? Mỗi phần thưởng có bao nhiêu quyển vở, bao nhiêu bút chì và bao nhiêu tập giấy?
Xem đáp án »
12/07/2024
5,736
Câu 3:
Cho các số x, y thõa mãn đẳng thức 3x2 + 3y2 + 4xy + 2x – 2y + 2 = 0.
Tính M = (x + y)2010 + (x + 2)2011 + (y – 1)2012.
Cho các số x, y thõa mãn đẳng thức 3x2 + 3y2 + 4xy + 2x – 2y + 2 = 0.
Tính M = (x + y)2010 + (x + 2)2011 + (y – 1)2012.
Xem đáp án »
12/07/2024
3,445
Câu 4:
Cho 1000 điểm phân biệt trong đó có đúng 3 điểm thẳng hàng. Hỏi có bao nhiêu đường thẳng tạo bởi 2 trong 1000 điểm đó?
Xem đáp án »
12/07/2024
3,205
Câu 5:
Tìm x:
a) 4x(3x – 7) – 6(2x2 – 5x + 1) = 12
b) (5x + 3)(4x – 1) + (10x – 7)(–2x + 3) = 27
c) (8x – 5)(3x + 2) – (12x + 7)(2x – 1) = 17
d) (5x + 9)(6x – 1) – (2x – 3)(15x + 1) = – 190.
Tìm x:
a) 4x(3x – 7) – 6(2x2 – 5x + 1) = 12
b) (5x + 3)(4x – 1) + (10x – 7)(–2x + 3) = 27
c) (8x – 5)(3x + 2) – (12x + 7)(2x – 1) = 17
d) (5x + 9)(6x – 1) – (2x – 3)(15x + 1) = – 190.
Xem đáp án »
12/07/2024
3,160
Câu 6:
Cho tam giác ABC. Trên cạnh AB lấy điểm M sao cho \(BM = \frac{1}{3}AB\), trên cạnh AC lấy điểm N sao cho \(CN = \frac{1}{3}AC\). Nối B với N, C với M, hai đoạn thẳng BN và CM cắt nhau tại O. Hãy so sánh diện tích tam giác OMB và ONC.
Cho tam giác ABC. Trên cạnh AB lấy điểm M sao cho \(BM = \frac{1}{3}AB\), trên cạnh AC lấy điểm N sao cho \(CN = \frac{1}{3}AC\). Nối B với N, C với M, hai đoạn thẳng BN và CM cắt nhau tại O. Hãy so sánh diện tích tam giác OMB và ONC.
Xem đáp án »
12/07/2024
2,992
Câu 7:
Trung bình cộng của hai số là 12,35. Tìm hai số đó biết rằng hiệu của chúng bằng 3,3.
Trung bình cộng của hai số là 12,35. Tìm hai số đó biết rằng hiệu của chúng bằng 3,3.
Xem đáp án »
12/07/2024
2,816
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
80 câu Bài tập Hình học Khối đa diện có lời giải chi tiết (P1)
-
148 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu từ đề thi Đại học có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận