Cho đoạn thẳng AB, O là trung điểm AB. Trên cùng 1 nửa mặt phẳng bờ AB, vẽ các tia Ax và By vuông góc với AB. Gọi C là 1 điểm thuộc tia Ax. Đường vuông góc với OC cắt By tại D. Chứng minh rằng CD = AC + BD.
Cho đoạn thẳng AB, O là trung điểm AB. Trên cùng 1 nửa mặt phẳng bờ AB, vẽ các tia Ax và By vuông góc với AB. Gọi C là 1 điểm thuộc tia Ax. Đường vuông góc với OC cắt By tại D. Chứng minh rằng CD = AC + BD.
Quảng cáo
Trả lời:
Giải bởi Vietjack
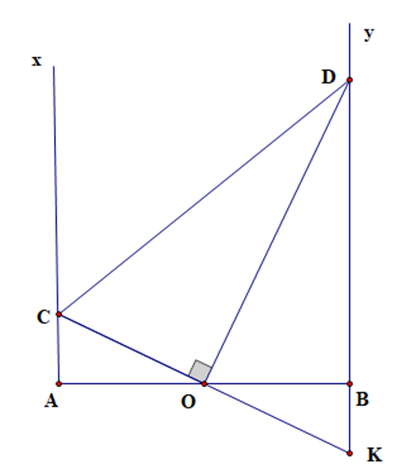
Gọi K là giao điểm của CO cà BD
Vì O là trung điểm của AB nên OA = OB
Vì Ax ⊥ AB nên \(\widehat {CAO} = 90^\circ \)
Vì By ⊥ AB nên \(\widehat {KBO} = 90^\circ \)
Xét △AOC và △BOK có
\(\widehat {CAO} = \widehat {KBO}\left( { = 90^\circ } \right)\)
OA = OB (chứng minh trên)
\(\widehat {COA} = \widehat {BOK}\) (hai góc đối đỉnh)
Do đó △AOC = △BOK (g.c.g)
Suy ra OC = OK, AC = BK (các cặp cạnh tương ứng)
Xét △DOC và △DOK có
OC = OK (chứng minh trên)
\(\widehat {COD} = \widehat {DOK}\left( { = 90^\circ } \right)\)
OD là cạnh chung
Do đó △DOC = △DOK (c.g.c)
Suy ra CD = DK (hai cạnh tương ứng)
Ta có CD = DK = BD + BK = BD + AC
Vậy CD = AC + BD.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Diện tích một mặt của hình lập phương là:
54 : 6 = 9 (cm2)
Vì 9 = 3 × 3 nên cạnh hình lập phương là 3 cm
Thể tích của hình lập phương là :
3 × 3 × 3 = 27 (cm3)
Vậy thể tích hình lập phương đó là 27 cm3.
Lời giải
Gọi số phần thưởng có thể chia được là x (phần thưởng) (x ∈ ℕ*)
Vì chia 128 quyển vở, 48 bút chì, 192 tập giấy thành 1 số phần thưởng như nhau
Nên x là ƯC(128, 48, 192)
Nhưng để x là nhiều nhất thì x = ƯCLN(128, 48, 192)
Ta có: 128 = 27; 48 = 24.3; 192 = 26.3
Suy ra ƯCLN(128, 48, 192) = 24 = 16
Do đó x = 16
Vậy chia được là 16 phần thưởng
Khi đó, mỗi phần thưởng có 128 : 16 = 8 (quyển vở); 48 : 16 = 3 (bút chì) và 192 : 16 = 12 (tập giấy).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo