Câu hỏi:
12/07/2024 1,110
Cho đường tròn (O) và dây cung AB của (O) không là đường kính. Gọi I là trung điểm của AB. Một đường thẳng thay đổi đi qua A cắt đường tròn tâm O bán kính OI tại P và Q.
a) Chứng minh rằng AP . AQ = AI2.
b) Giả sử đường tròn ngoại tiếp tam giác BPQ cắt AB tại K khác B. Chứng minh
rằng AK . AB = AP . AQ.
c) Chứng minh rằng K là trung điểm của AI.
Cho đường tròn (O) và dây cung AB của (O) không là đường kính. Gọi I là trung điểm của AB. Một đường thẳng thay đổi đi qua A cắt đường tròn tâm O bán kính OI tại P và Q.
a) Chứng minh rằng AP . AQ = AI2.
b) Giả sử đường tròn ngoại tiếp tam giác BPQ cắt AB tại K khác B. Chứng minh
rằng AK . AB = AP . AQ.
c) Chứng minh rằng K là trung điểm của AI.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Bắt đầu thiQuảng cáo
Trả lời:
Giải bởi Vietjack
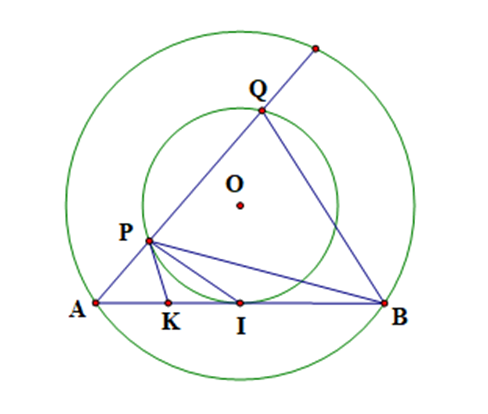
a) Xét (O; OA) có I là trung điểm của dây cung AB, suy ra OI ⊥ AB
Xét (O; OI) có OI ⊥ AI
Suy ra AI là tiếp tuyến của (O; OI) tại I
Do đó \(\widehat {PIA} = \widehat {PQI}\) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung PI)
Xét DAIP và DAQI có
\(\widehat {PIA} = \widehat {PQI}\) (chứng minh trên);
\(\widehat {PAI}\) là góc chung
Suy ra (g.g)
Do đó \(\frac{{AI}}{{AQ}} = \frac{{AP}}{{AI}}\), suy ra AP . AQ = AI2
b) Vì BKPQ là tứ giác nội tiếp nên \(\widehat {APK} = \widehat {KBQ}\)
Xét DAPK và DABQ có
\(\widehat {APK} = \widehat {ABQ}\) (chứng minh trên);
\(\widehat {PAK}\) là góc chung
Suy ra (g.g)
Do đó \(\frac{{AP}}{{AB}} = \frac{{AK}}{{AQ}}\), suy ra AP . AQ = AB . AK.
c) Ta có AP . AQ = AB . AK (chứng minh câu b)
AP . AQ = AI2 (chứng minh câu a)
Suy ra AB . AK = AI2
⇔ 2AI . AK = AI2 (vì I là trung điểm của AB)
⇔ 2AK = AI
\( \Rightarrow AK = \frac{1}{2}AI\)
Vậy K là trung điểm của AI.
Nhà sách vietjack
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Hình lập phương có diện tích toàn phần là 54 cm2 . Tính thể tích hình đó.
Hình lập phương có diện tích toàn phần là 54 cm2 . Tính thể tích hình đó.
Xem đáp án »
12/07/2024
6,032
Câu 2:
Giáo viên chủ nhiệm muốn chia 128 quyền vở; 48 bút chì và 192 tập giấy thành một số phần thưởng như nhau cho các học sinh giỏi nhân dịp tổng kết năm học. Hỏi có thể chia nhiều nhất là bao nhiêu phần thưởng? Mỗi phần thưởng có bao nhiêu quyển vở, bao nhiêu bút chì và bao nhiêu tập giấy?
Xem đáp án »
12/07/2024
5,706
Câu 3:
Cho các số x, y thõa mãn đẳng thức 3x2 + 3y2 + 4xy + 2x – 2y + 2 = 0.
Tính M = (x + y)2010 + (x + 2)2011 + (y – 1)2012.
Cho các số x, y thõa mãn đẳng thức 3x2 + 3y2 + 4xy + 2x – 2y + 2 = 0.
Tính M = (x + y)2010 + (x + 2)2011 + (y – 1)2012.
Xem đáp án »
12/07/2024
3,367
Câu 4:
Cho 1000 điểm phân biệt trong đó có đúng 3 điểm thẳng hàng. Hỏi có bao nhiêu đường thẳng tạo bởi 2 trong 1000 điểm đó?
Xem đáp án »
12/07/2024
3,107
Câu 5:
Tìm x:
a) 4x(3x – 7) – 6(2x2 – 5x + 1) = 12
b) (5x + 3)(4x – 1) + (10x – 7)(–2x + 3) = 27
c) (8x – 5)(3x + 2) – (12x + 7)(2x – 1) = 17
d) (5x + 9)(6x – 1) – (2x – 3)(15x + 1) = – 190.
Tìm x:
a) 4x(3x – 7) – 6(2x2 – 5x + 1) = 12
b) (5x + 3)(4x – 1) + (10x – 7)(–2x + 3) = 27
c) (8x – 5)(3x + 2) – (12x + 7)(2x – 1) = 17
d) (5x + 9)(6x – 1) – (2x – 3)(15x + 1) = – 190.
Xem đáp án »
12/07/2024
3,064
Câu 6:
Trung bình cộng của hai số là 12,35. Tìm hai số đó biết rằng hiệu của chúng bằng 3,3.
Trung bình cộng của hai số là 12,35. Tìm hai số đó biết rằng hiệu của chúng bằng 3,3.
Xem đáp án »
12/07/2024
2,740
Câu 7:
Cho tam giác ABC. Trên cạnh AB lấy điểm M sao cho \(BM = \frac{1}{3}AB\), trên cạnh AC lấy điểm N sao cho \(CN = \frac{1}{3}AC\). Nối B với N, C với M, hai đoạn thẳng BN và CM cắt nhau tại O. Hãy so sánh diện tích tam giác OMB và ONC.
Cho tam giác ABC. Trên cạnh AB lấy điểm M sao cho \(BM = \frac{1}{3}AB\), trên cạnh AC lấy điểm N sao cho \(CN = \frac{1}{3}AC\). Nối B với N, C với M, hai đoạn thẳng BN và CM cắt nhau tại O. Hãy so sánh diện tích tam giác OMB và ONC.
Xem đáp án »
12/07/2024
2,709
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)
-
124 câu Trắc nghiệm Ôn tập Toán 12 Chương 3 Hình học có đáp án (Phần 1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận