Câu hỏi:
12/07/2024 2,023
Cho hình thang ABCD (AB // CD). Gọi M, N, P, Q theo thứ tự là trung điểm của AB, AC, CD, BD
a) Chứng minh rằng MNPQ là hình bình hành
b) Hình thang ABCD phải có thêm điều kiện gì để tứ giác MPNQ là hình thoi.
Cho hình thang ABCD (AB // CD). Gọi M, N, P, Q theo thứ tự là trung điểm của AB, AC, CD, BD
a) Chứng minh rằng MNPQ là hình bình hành
b) Hình thang ABCD phải có thêm điều kiện gì để tứ giác MPNQ là hình thoi.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
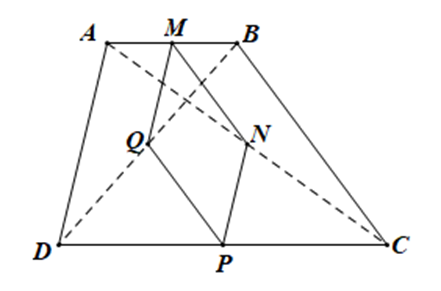
a) Xét tam giác BAD có: M, Q lần lượt là trung điểm của AB, BD
Suy ra MQ là đường trung bình của tam giác BAD
Do đó MQ // AD và \(MQ = \frac{1}{2}A{\rm{D}}\) (1)
Xét tam giác CAD có: N, P lần lượt là trung điểm của AC, CD
Suy ra NP là đường trung bình của tam giác CAD
Do đó NP // AD và \(NP = \frac{1}{2}A{\rm{D}}\) (2)
Từ (1) và (2) suy ra MQ // NP ; MQ = NP
Xét tứ giác MNPQ có: MQ // NP ; MQ = NP (chứng minh trên)
Suy ra MNPQ là hình bình hành
b) Xét tam giác CAB có: N, M là trung điểm của AC, AB
Suy ra NM là đường trung bình của tam giác CAB
Do đó \(NM = \frac{1}{2}BC\)
Để MPNQ là hình thoi ⇔ MN = MQ
⇔ AD = BC (vì \(MQ = \frac{1}{2}A{\rm{D,}}MN = \frac{1}{2}BC\))
⇔ Hình thang ABCD là hình thang cân
Vậy hình thang ABCD cân thì MNPQ là hình bình hành.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới)
Đã bán 1,5k
₫ 70.000
₫ 36.000
Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025)
Đã bán 1,1k
₫ 70.000
₫ 36.000
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Hình lập phương có diện tích toàn phần là 54 cm2 . Tính thể tích hình đó.
Hình lập phương có diện tích toàn phần là 54 cm2 . Tính thể tích hình đó.
Xem đáp án »
12/07/2024
7,004
Câu 2:
Giáo viên chủ nhiệm muốn chia 128 quyền vở; 48 bút chì và 192 tập giấy thành một số phần thưởng như nhau cho các học sinh giỏi nhân dịp tổng kết năm học. Hỏi có thể chia nhiều nhất là bao nhiêu phần thưởng? Mỗi phần thưởng có bao nhiêu quyển vở, bao nhiêu bút chì và bao nhiêu tập giấy?
Xem đáp án »
12/07/2024
5,739
Câu 3:
Cho các số x, y thõa mãn đẳng thức 3x2 + 3y2 + 4xy + 2x – 2y + 2 = 0.
Tính M = (x + y)2010 + (x + 2)2011 + (y – 1)2012.
Cho các số x, y thõa mãn đẳng thức 3x2 + 3y2 + 4xy + 2x – 2y + 2 = 0.
Tính M = (x + y)2010 + (x + 2)2011 + (y – 1)2012.
Xem đáp án »
12/07/2024
3,454
Câu 4:
Cho 1000 điểm phân biệt trong đó có đúng 3 điểm thẳng hàng. Hỏi có bao nhiêu đường thẳng tạo bởi 2 trong 1000 điểm đó?
Xem đáp án »
12/07/2024
3,209
Câu 5:
Tìm x:
a) 4x(3x – 7) – 6(2x2 – 5x + 1) = 12
b) (5x + 3)(4x – 1) + (10x – 7)(–2x + 3) = 27
c) (8x – 5)(3x + 2) – (12x + 7)(2x – 1) = 17
d) (5x + 9)(6x – 1) – (2x – 3)(15x + 1) = – 190.
Tìm x:
a) 4x(3x – 7) – 6(2x2 – 5x + 1) = 12
b) (5x + 3)(4x – 1) + (10x – 7)(–2x + 3) = 27
c) (8x – 5)(3x + 2) – (12x + 7)(2x – 1) = 17
d) (5x + 9)(6x – 1) – (2x – 3)(15x + 1) = – 190.
Xem đáp án »
12/07/2024
3,161
Câu 6:
Cho tam giác ABC. Trên cạnh AB lấy điểm M sao cho \(BM = \frac{1}{3}AB\), trên cạnh AC lấy điểm N sao cho \(CN = \frac{1}{3}AC\). Nối B với N, C với M, hai đoạn thẳng BN và CM cắt nhau tại O. Hãy so sánh diện tích tam giác OMB và ONC.
Cho tam giác ABC. Trên cạnh AB lấy điểm M sao cho \(BM = \frac{1}{3}AB\), trên cạnh AC lấy điểm N sao cho \(CN = \frac{1}{3}AC\). Nối B với N, C với M, hai đoạn thẳng BN và CM cắt nhau tại O. Hãy so sánh diện tích tam giác OMB và ONC.
Xem đáp án »
12/07/2024
3,047
Câu 7:
Trung bình cộng của hai số là 12,35. Tìm hai số đó biết rằng hiệu của chúng bằng 3,3.
Trung bình cộng của hai số là 12,35. Tìm hai số đó biết rằng hiệu của chúng bằng 3,3.
Xem đáp án »
12/07/2024
2,817
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
80 câu Bài tập Hình học Khối đa diện có lời giải chi tiết (P1)
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
148 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu từ đề thi Đại học có lời giải (P1)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận