Câu hỏi:
07/06/2023 955
Cho (O; R). Từ điểm A nằm ngoài (O; R), vẽ hai tiếp tuyến AM và AN với đường tròn (M và N là các tiếp điểm). Vẽ dây NC của (O; R) vuông góc với MB tại H. Gọi I là giao điểm của AB và NH. Tính tỉ số \(\frac{{NI}}{{NC}}\).
Cho (O; R). Từ điểm A nằm ngoài (O; R), vẽ hai tiếp tuyến AM và AN với đường tròn (M và N là các tiếp điểm). Vẽ dây NC của (O; R) vuông góc với MB tại H. Gọi I là giao điểm của AB và NH. Tính tỉ số \(\frac{{NI}}{{NC}}\).
Câu hỏi trong đề:
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
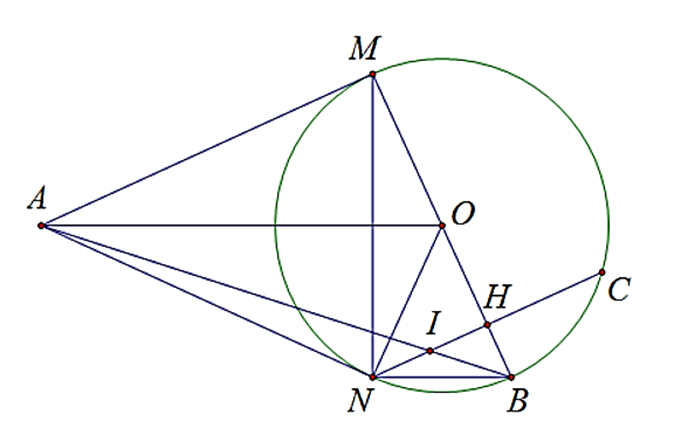
Ta có:
MA ⊥ MB (tiếp tuyến vuông góc với đường kính)
NC ⊥ OB suy ra: IH ⊥ MB
Do đó: IH // MA
Áp dụng định lí Thalès trong tam giác MAB có:
\(\frac{{HB}}{{MB}} = \frac{{IB}}{{BA}} = \frac{{IH}}{{MA}}\,\,hay\,\,\frac{{HI}}{{MA}} = \frac{{HB}}{{MB}} = \frac{{HB}}{{2MO}}\,\)(1)
Ta có: AMON là tứ giác nội tiếp đường tròn vì \[\widehat {ANO} + \widehat {AMO}\] = 180° suy ra: \[\widehat {MNO} = \widehat {MAO}\]
Mà \[\widehat {ONB}\, + \widehat {MON}\, = \widehat {MAO\,} + \,\widehat {MOA}\,\]= 90°
Suy ra: \[\widehat {ONB}\,\, = \,\,\widehat {MOA}\,\]
Mặt khác tam giác ONB cân tại O nên \[\widehat {ONB}\,\, = \,\,\widehat {HBN}\,\]
Xét tam giác HBN và tam giác MOA có:
\(\widehat {NHB} = \widehat {AMO}\)= 90°
\(\widehat {HBN} = \widehat {ONB} = \widehat {MOA}\)
Suy ra: ∆HBN ᔕ ∆MOA (g.g)
Hay \(\frac{{HN}}{{MA}} = \frac{{HB}}{{MO}} = \frac{{2HB}}{{MB}}\,\,\)(2)
Từ (1) và (2) suy ra: \(\frac{{HN}}{{MA}} = \frac{{2HI}}{{MA}}\,\,\)hay HN = 2HI = 2NI
Mà NC = 2HN
Suy ra: NC = 4NI
Vậy \[\frac{{NI}}{{NC}} = \frac{1}{4}\].
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Một người dự định đi bộ quãng đường với vận tốc 5km/h nhưng khi đi được nửa đường thì nhờ được bạn đèo xe đạp đi tiếp với vận tốc 12km/h do đó đến sớm hơn dự định 28 phút. Hỏi người ấy đi hết toàn bộ quãng đường trong bao lâu ?
Một người dự định đi bộ quãng đường với vận tốc 5km/h nhưng khi đi được nửa đường thì nhờ được bạn đèo xe đạp đi tiếp với vận tốc 12km/h do đó đến sớm hơn dự định 28 phút. Hỏi người ấy đi hết toàn bộ quãng đường trong bao lâu ?
Xem đáp án »
08/06/2023
7,850
Câu 2:
Một miếng đất hình chữ nhật có chu vi 80m. Nếu chiều rộng tăng thêm 5 m, chiều dài tăng thêm 3m thì diện tích tăng 195 m2. Tính kích thước của mảnh đất?
Một miếng đất hình chữ nhật có chu vi 80m. Nếu chiều rộng tăng thêm 5 m, chiều dài tăng thêm 3m thì diện tích tăng 195 m2. Tính kích thước của mảnh đất?
Xem đáp án »
13/07/2024
7,679
Câu 4:
Một đội công nhân có 63 người nhận sửa xong một quãng đường trong 11 ngày. Hỏi muốn làm xong quãng đường đó trong 7 ngày thì cần thêm bao nhiêu người nữa ? (Mức làm của mỗi người như nhau).
Một đội công nhân có 63 người nhận sửa xong một quãng đường trong 11 ngày. Hỏi muốn làm xong quãng đường đó trong 7 ngày thì cần thêm bao nhiêu người nữa ? (Mức làm của mỗi người như nhau).
Xem đáp án »
08/06/2023
5,616
Câu 5:
Cho tam giác ABC. Trên tia đối của tia AC lấy điểm D sao cho AD = AC. Kẻ DE và CF cùng vuông góc với đường thẳng AB ở E và F.
a) Chứng minh: A là trung điểm của EF.
b) Chứng minh: DF // CE.
Cho tam giác ABC. Trên tia đối của tia AC lấy điểm D sao cho AD = AC. Kẻ DE và CF cùng vuông góc với đường thẳng AB ở E và F.
a) Chứng minh: A là trung điểm của EF.
b) Chứng minh: DF // CE.
Xem đáp án »
13/07/2024
5,465
Câu 6:
Cho xyz = 1 và x + y + z = \(\frac{1}{x} + \frac{1}{y} + \frac{1}{z}\). Chứng minh rằng trong 3 số x, y, z có ít nhất 1 số bằng 1.
Cho xyz = 1 và x + y + z = \(\frac{1}{x} + \frac{1}{y} + \frac{1}{z}\). Chứng minh rằng trong 3 số x, y, z có ít nhất 1 số bằng 1.
Xem đáp án »
08/06/2023
5,286
Câu 7:
Lớp 4a có 28 học sinh. Số học sinh nam nhiều hơn số học sinh nữ là 4 em. Hỏi lớp 4a có bao nhiêu học sinh nam, bao nhiêu học sinh nữ?
Lớp 4a có 28 học sinh. Số học sinh nam nhiều hơn số học sinh nữ là 4 em. Hỏi lớp 4a có bao nhiêu học sinh nam, bao nhiêu học sinh nữ?
Xem đáp án »
08/06/2023
4,943
Bình luận
🔥 Đề thi HOT:
-
53 câu Bài tập về Tính đơn điệu của hàm số có lời giải (P1)
-
7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 1)
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
200 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số nâng cao (P1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)
về câu hỏi!