Câu hỏi:
13/07/2024 7,205
Số học sinh của một trường là một số tự nhiên có 3 chữ số và lớn hơn 900. Mỗi lần xếp hàng 3, hàng 4, hàng 5 đều không có ai lẻ hàng. Tính số học sinh của trường đó?
Số học sinh của một trường là một số tự nhiên có 3 chữ số và lớn hơn 900. Mỗi lần xếp hàng 3, hàng 4, hàng 5 đều không có ai lẻ hàng. Tính số học sinh của trường đó?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi số học sinh của trường đó là x (900 < x < 1000 và x ∈ ℕ).
Mỗi lần xếp hàng 3, hàng 4, hàng 5 đều không có ai lẻ hàng.
Suy ra x chia hết cho 3, 4, 5 hay x là BC(3, 4, 5).
Mà BCNN(3, 4, 5) = 60.
Do đó x ∈ B(60) = {0; 60; 120; 180; 240; 300; ...}.
Mà 900 < x < 1000 và x ∈ ℕ nên x = 960.
Vậy số học sinh của trường đó là 960.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đặt A = 1.2 + 2.3 + 3.4 + ... + 98.99.
Suy ra 3A = 1.2.3 + 2.3.3 + 3.4.3 + ... + 98.99.3.
= 1.2.3 + 2.3.(4 – 1) + 3.4.(5 – 2) + ... + 98.99.(100 – 97).
= 1.2.3 + 2.3.4 – 1.2.3 + 3.4.5 – 2.3.4 + ... + 98.99.100 – 97.98.99.
= 98.99.100
Suy ra A = 98.99.100 : 3 = 98.33.100 = 323 400.
Vậy A = 323 400.
Lời giải
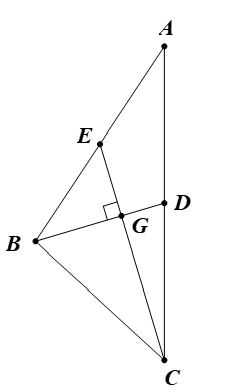
Ta có D, E lần lượt là trung điểm của AC, AB.
Suy ra .
Gọi G là giao điểm của CE và BD.
Suy ra G là trọng tâm của tam giác ABC.
Đặt GD = x, GE = y.
Áp dụng tính chất trọng tâm cho tam giác ABC, ta được:
⦁ . Suy ra BG = 2GD = 2x.
⦁ . Suy ra CG = 2GE = 2y.
Áp dụng định lí Pitago cho tam giác BGE vuông tại G: BG2 + GE2 = BE2.
⇔ 4x2 + y2 = 9 (1)
Áp dụng định lí Pitago cho tam giác CGD vuông tại G: CG2 + GD2 = CD2.
⇔ 4y2 + x2 = 16 (2)
Lấy (1) + (2) vế theo vế, ta được 5(x2 + y2) = 25.
⇔ x2 + y2 = 5.
Áp dụng định lí Pitago cho tam giác BGC vuông tại G: BG2 + CG2 = BC2.
⇔ 4x2 + 4y2 = BC2.
⇔ 4(x2 + y2) = BC2.
⇔ BC2 = 4.5 = 20.
Vậy .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
140 câu Bài tập Hàm số mũ và Logarit cơ bản, nâng cao cực hay có lời giải chi tiết (P1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận