Lấy điểm A trên (O; R), vẽ tiếp tuyến Ax. Trên Ax lấy điểm B. Trên (O; R) lấy điểm C sao cho BC = AB.
a) Chứng minh CB là tiếp tuyến của (O).
b) Vẽ đường kính AD của (O), kẻ CK vuông góc với AD. Chứng minh rằng CD // OB và BC.CD = CK.OB.
c) Lấy điểm M trên cung nhỏ AC của (O). Vẽ tiếp tuyến tại M cắt AB, BC lần lượt tại E, F. Vẽ đường tròn tâm I nội tiếp ∆BEF. Chứng minh .
Lấy điểm A trên (O; R), vẽ tiếp tuyến Ax. Trên Ax lấy điểm B. Trên (O; R) lấy điểm C sao cho BC = AB.
a) Chứng minh CB là tiếp tuyến của (O).
b) Vẽ đường kính AD của (O), kẻ CK vuông góc với AD. Chứng minh rằng CD // OB và BC.CD = CK.OB.
c) Lấy điểm M trên cung nhỏ AC của (O). Vẽ tiếp tuyến tại M cắt AB, BC lần lượt tại E, F. Vẽ đường tròn tâm I nội tiếp ∆BEF. Chứng minh .
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
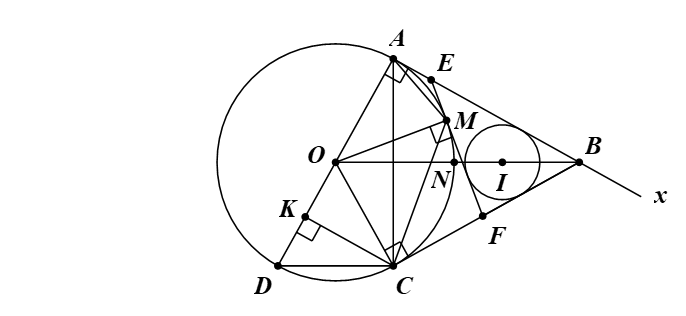
a) Ta có \(\widehat {OAB} = 90^\circ \) (do AB là tiếp tuyến của (O)).
Xét ∆ABO và ∆CBO, có:
OB chung;
AB = BC (giả thiết);
OA = OC (= R).
Do đó ∆ABO = ∆CBO (c.c.c).
Suy ra \(\widehat {OCB} = \widehat {OAB} = 90^\circ \).
Vậy CB là tiếp tuyến của (O).
b) Gọi N là giao điểm của OB và (O).
Ta có \(\widehat {AOB} = \widehat {BOC}\) (∆ABO = ∆CBO).
Suy ra sđ = sđ.
Lại có \(\widehat {AOB}\) = sđ và \(\widehat {ODC} = \frac{1}{2}\)sđ = sđ.
Do đó \(\widehat {AOB} = \widehat {ODC}\).
Mà hai góc này ở vị trí đồng vị.
Vậy CD // OB.
Xét ∆OBC và ∆DCK, có:
\(\widehat {BOC} = \widehat {KDC}\,\,\left( { = \widehat {OCD}} \right)\);
\(\widehat {OCB} = \widehat {CKD} = 90^\circ \).
Do đó (g.g).
Suy ra \(\frac{{BC}}{{CK}} = \frac{{OB}}{{CD}}\).
Vậy BC.CD = CK.OB.
c) Ta có I là tâm đường tròn nội tiếp tam giác BEF.
Suy ra EI là tia phân giác của \(\widehat {BEF}\).
Do đó \(\widehat {IEF} = \frac{1}{2}\widehat {BEF}\) (1)
Tứ giác EAOM, có: \(\widehat {EAO} = \widehat {EMO} = 90^\circ \) (AE, ME là tiếp tuyến của (O)).
Suy ra \(\widehat {EAO} + \widehat {EMO} = 180^\circ \).
Do đó tứ giác EAOM nội tiếp đường tròn đường kính OE.
Vì vậy \(\widehat {BEF} = \widehat {AOM}\) (2)
Đường tròn (O; R), có: \(\widehat {AOM}\) là góc ở tâm chắn và \(\widehat {MCA}\) là góc nội tiếp chắn .
Suy ra \(\widehat {AOM} = 2\widehat {MCA}\) (3)
Từ (1), (2), (3), suy ra \(\widehat {IEF} = \widehat {MCA}\).
Chứng minh tương tự, ta được: \(\widehat {IFE} = \widehat {MAC}\).
Xét ∆MAC và ∆IFE, có:
\(\widehat {IEF} = \widehat {MCA}\) (chứng minh trên);
\(\widehat {IFE} = \widehat {MAC}\) (chứng minh trên).
Vậy (g.g).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
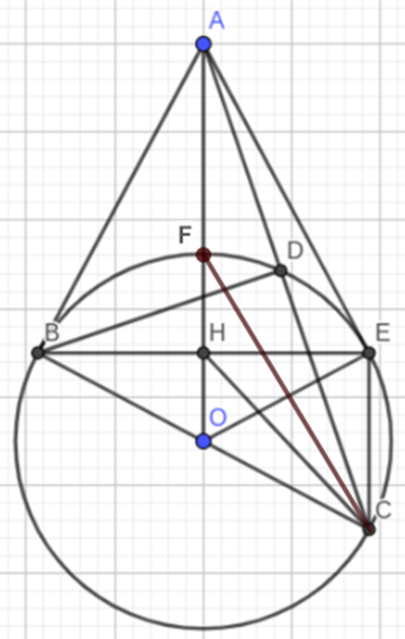
a) Vì D thuộc đường tròn (O) và BC là đường kính nên \(\widehat {BDC} = 90^\circ \).
Suy ra BD ⊥ AC.
Ta có AB là tiếp tuyến của (O), với B là tiếp điểm.
Suy ra \(\widehat {ABC} = 90^\circ \).
Tam giác ABC vuông tại B có BD là đường cao: AB2 = AD.AC (Hệ thức lượng trong tam giác vuông).
Vậy BD vuông góc AC và AB2 = AD.AC.
b) Xét tam giác BEC có O là trung điểm BC (do BC là đường kính của (O)) và OH // CE (giả thiết).
Suy ra OH là đường trung bình của tam giác BEC.
Vậy H là trung điểm của BE.
Vì E thuộc đường tròn (O) và BC là đường kính nên \(\widehat {BEC} = 90^\circ \).
Suy ra BE ⊥ CE.
Mà CE // OH (giả thiết).
Do đó OH ⊥ BE hay AH ⊥ BE.
Tam giác ABE có AH vừa là đường trung tuyến, vừa là đường cao.
Suy ra tam giác ABE cân tại A.
Do đó AB = AE.
Xét ∆ABO và ∆AEO, có:
AO chung;
AB = AE (chứng minh trên);
OB = OE (= R).
Do đó ∆ABO = ∆AEO (c.c.c).
Suy ra \(\widehat {AEO} = \widehat {ABO} = 90^\circ \) (cặp góc tương ứng).
Vậy AE là tiếp tuyến của (O).
c) Tam giác OBA vuông tại B có BH là đường cao: OB2 = OH.OA (Hệ thức lượng trong tam giác vuông).
Suy ra OC2 = OH.OA.
Xét ∆OHC và ∆OCA, có:
\(\frac{{OH}}{{OC}} = \frac{{OC}}{{OA}}\) (OC2 = OH.OA);
\(\widehat {COH}\) chung.
Do đó (c.g.c).
Vậy \(\widehat {OCH} = \widehat {OAC}\) (cặp góc tương ứng).
d) Ta có \(\widehat {OCF} = \widehat {FCE}\,\,\left( { = \widehat {OFC}} \right)\).
Lại có \(\widehat {OCH} = \widehat {ACE}\,\,\left( { = \widehat {OAC}} \right)\).
Suy ra \(\widehat {HCF} = \widehat {FCA}\).
Khi đó CF là tia phân giác của \(\widehat {HCA}\).
Áp dụng tính chất đường phân giác cho tam giác HCA, ta được: \(\frac{{HF}}{{FA}} = \frac{{HC}}{{CA}}\).
Vậy FA.CH = HF.CA (điều phải chứng minh).
Lời giải
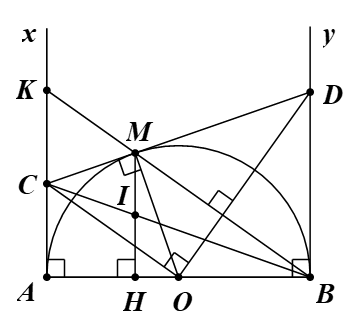
a) Đường tròn (O) có hai tiếp tuyến AC, MC cắt nhau tại C.
Suy ra OC là tia phân giác của \(\widehat {AOM}\) (tính chất hai tiếp tuyến cắt nhau).
Do đó \(2\widehat {AOC} = 2\widehat {COM} = \widehat {AOM}\).
Chứng minh tương tự, ta được \(2\widehat {MOD} = 2\widehat {DOB} = \widehat {MOB}\).
Ta có \(\widehat {AOM} + \widehat {MOB} = 180^\circ \) (kề bù).
Suy ra \(2\widehat {COM} + 2\widehat {MOD} = 180^\circ \).
Khi đó \(2\left( {\widehat {COM} + \widehat {MOD}} \right) = 180^\circ \).
Vì vậy \(\widehat {COD} = 180^\circ :2 = 90^\circ \).
Vậy tam giác COD vuông tại O.
b) Đường tròn (O) có hai tiếp tuyến AC, MC cắt nhau tại C.
Suy ra AC = MC (tính chất hai tiếp tuyến cắt nhau).
Chứng minh tương tự, ta được DM = BD.
Ta có CD là tiếp tuyến của (O) có M là tiếp điểm. Suy ra OM ⊥ CD.
Tam giác COD vuông tại O có OM là đường cao: OM2 = CM.DM.
⇔ R2 = AC.BD.
Vậy ta có điều phải chứng minh.
c) Gọi I là giao điểm của MH và BC, K là giao điểm của MB và AC.
Đường tròn (O) có hai tiếp tuyến DM, DB cắt nhau tại D.
Suy ra DM = DB.
Lại có OM = OB = R.
Suy ra OD là đường trung trực của đoạn MB.
Do đó OD ⊥ MB.
Mà OD ⊥ OC (tam giác COD vuông tại O).
Suy ra MB // OC.
Mà O là trung điểm AB (đường tròn (O) có AB là đường kính).
Do đó OC là đường trung bình của tam giác ABK.
Vì vậy C là trung điểm AK.
Ta có MH ⊥ AB (giả thiết) và AK ⊥ AB (do AK là tiếp tuyến của (O) tại A).
Suy ra MH // AK.
Áp dụng định lí Thales, ta được \(\frac{{MI}}{{CK}} = \frac{{IH}}{{AC}} = \frac{{BI}}{{BC}}\).
Mà CK = CA (C là trung điểm AK).
Suy ra MI = IH.
Do đó I là trung điểm của MH.
Vậy BC đi qua trung điểm I của đoạn MH.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(\frac{{57}}{{16}}\).
B. \(\frac{{16}}{{57}}\).
C. \( - \frac{{57}}{{16}}\).
D. \( - \frac{{16}}{{57}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.