Cho tam giác ABC đều cạnh a. Gọi M, N là các điểm sao cho \(3\overrightarrow {BM} = 2\overrightarrow {BC} ,5\overrightarrow {AN} = 4\overrightarrow {AC} .\)
a) Tính \(\overrightarrow {AB} .\overrightarrow {AC} ,\,\,\overrightarrow {BC} .\overrightarrow {AC} .\)
b) Chứng minh AM vuông góc với BN.
Cho tam giác ABC đều cạnh a. Gọi M, N là các điểm sao cho \(3\overrightarrow {BM} = 2\overrightarrow {BC} ,5\overrightarrow {AN} = 4\overrightarrow {AC} .\)
a) Tính \(\overrightarrow {AB} .\overrightarrow {AC} ,\,\,\overrightarrow {BC} .\overrightarrow {AC} .\)
b) Chứng minh AM vuông góc với BN.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
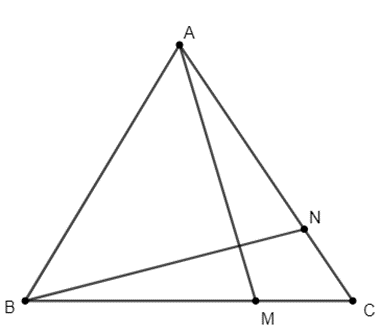
a) Ta có: \(\overrightarrow {AB} .\overrightarrow {AC} = AB.AC.\cos \widehat {BAC} = a.a.\cos 60^\circ = \frac{{{a^2}}}{2};\)
\(\overrightarrow {BC} .\overrightarrow {AC} = \overrightarrow {CB} .\overrightarrow {CA} = CB.CA.\cos \widehat {BCA} = a.a.\cos 60^\circ = \frac{{{a^2}}}{2}.\)
b) Ta có: \(3\overrightarrow {BM} = 2\overrightarrow {BC} \)
⇔ \(3\left( {\overrightarrow {AM} - \overrightarrow {AB} } \right) = 2\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right)\)
⇔ \(\overrightarrow {AM} = \frac{2}{3}\overrightarrow {AC} + \frac{1}{3}\overrightarrow {AB} \)
Ta có: \(5\overrightarrow {AN} = 4\overrightarrow {AC} \)
⇔ \(5\left( {\overrightarrow {BN} - \overrightarrow {BA} } \right) = 4\overrightarrow {AC} \)
⇔ \(\overrightarrow {BN} = - \overrightarrow {AB} + \frac{4}{5}\overrightarrow {AC} \)
Ta có: \(\overrightarrow {AM} .\overrightarrow {BN} = \left( {\frac{2}{3}\overrightarrow {AC} + \frac{1}{3}\overrightarrow {AB} } \right)\left( { - \overrightarrow {AB} + \frac{4}{5}\overrightarrow {AC} } \right)\)
\( = - \frac{2}{3}\overrightarrow {AC} .\overrightarrow {AB} + \frac{8}{{15}}{\overrightarrow {AC} ^2} - \frac{1}{3}{\overrightarrow {AB} ^2} + \frac{4}{{15}}\overrightarrow {AC} .\overrightarrow {AB} \)
\( = - \frac{2}{5}\overrightarrow {AC} .\overrightarrow {AB} + \frac{8}{{15}}{\overrightarrow {AC} ^2} - \frac{1}{3}{\overrightarrow {AB} ^2}\)
\( = - \frac{2}{3}.\frac{{{a^2}}}{2} + \frac{8}{{15}}{a^2} - \frac{1}{3}{a^2} = 0\)
⇒ AM ⊥ BN ⇒ AM vuông góc với BN.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
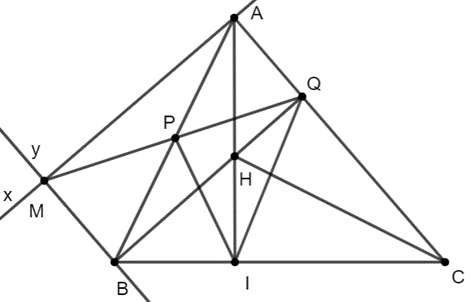
Vì Ax ⊥ AC ⇒ AM ⊥ AC
mà BM // AC
⇒ AM ⊥ BM
Chứng minh tương tự ⇒ AQ // BM và BM // AQ (cmt)
Suy ra AMBQ là hình bình hành.
Mà \(\widehat {AMB} = \widehat {MBQ} = \widehat {ABQ} = \widehat {MAQ} = {90^o}\).
Vậy AMBQ là hình chữ nhật.
b) BQ ⊥ AC (cmt) mà \(BQ \cap AI = H\)
Suy ra H là trực tâm của tam giác ABC.
Do đó: CH ⊥ AB
c) AMBQ là hình chữ nhật mà \(AB \cap QM = P\)
⇒ P là trung điểm AB và P là trung điểm QM
\(\Delta ABI\) vuông tại I có đường trung tuyến IP
⇒ \(IP = \frac{1}{2}AB\)
⇒ IP = PQ
⇒ \(\Delta IPQ\) cân tại P.
Lời giải
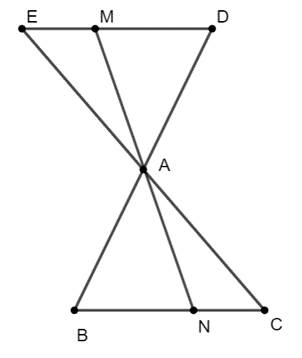
a) Xét \(\Delta ADE\) và \(\Delta ABC\) có:
AD = AB
\(\widehat {DAE} = \widehat {BAC}\) (2 góc đối đỉnh)
AC = AE
⇒ \(\Delta ADE = \Delta BAC\left( {c.g.c} \right)\)
⇒ \(\widehat {ADE} = \widehat {ABC}\) (2 góc tương ứng) mà chúng ở vị trí so le trong với nhau
⇒ BC // DE (đpcm)
b) Xét \(\Delta DAM\) và \(\Delta BAN\) có:
\(\widehat {DAM} = \widehat {BAN}\) (2 góc đối đỉnh)
AD = AB
\(\widehat {ABN} = \widehat {ADM}\) (CMT)
⇒ \(\Delta DAM = \Delta BAN\left( {g.c.g} \right)\)
⇒ AM = AN (2 cạnh tương ứng) (dpcm)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. −8;
B. \(3\sqrt {11} - 13\);
C. −39;
D. −21.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.