Từ một điểm M ở ngoài đường tròn (O), vẽ hai tiếp tuyến MA, MB đến đường tròn (A, B là hai tiếp điểm). Qua A vẽ đường thẳng song song với MB, cắt đường tròn tại E, đoạn thẳng ME cắt đường tròn tại F. Hai đường thẳng AF và MB cắt nhau tại I.
a) Chứng minh tứ giác MAOB nội tiếp đường tròn.
b) Chứng minh \(I{B^2} = IF.IA.\)
c) Chứng minh IB = IM.
Từ một điểm M ở ngoài đường tròn (O), vẽ hai tiếp tuyến MA, MB đến đường tròn (A, B là hai tiếp điểm). Qua A vẽ đường thẳng song song với MB, cắt đường tròn tại E, đoạn thẳng ME cắt đường tròn tại F. Hai đường thẳng AF và MB cắt nhau tại I.
a) Chứng minh tứ giác MAOB nội tiếp đường tròn.
b) Chứng minh \(I{B^2} = IF.IA.\)
c) Chứng minh IB = IM.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
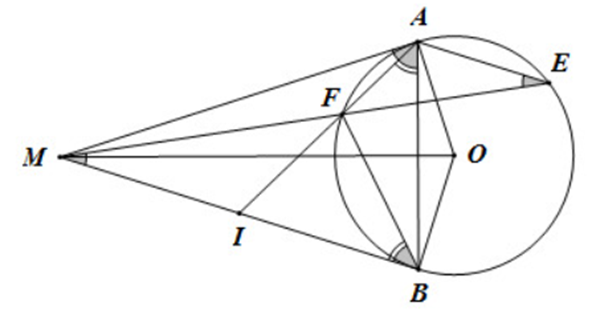
a) Vì MA, MB là tiếp tuyến của (O) nên MA ⊥ AO, MB ⊥ BO.
⇒ \(\widehat {MAO} = \widehat {MBO} = 90^\circ \)
⇒ \(\widehat {MAO} + \widehat {MBO} = 180^\circ \)
⇒ MAOB là tứ giác nội tiếp đường tròn (dpcm)
b) Ta có: \(\widehat {FAB} = \widehat {FBI}\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung BF)
Xét \(\Delta IAB\) và \(\Delta IBF\) có:
\(\widehat {IAB} = \widehat {IBF}\left( {cmt} \right)\)
\(\widehat {AIB}\) chung
Do đó \(\Delta IAB\) ᔕ \(\Delta IBF\left( {g.g} \right)\)
Suy ra \(\frac{{IA}}{{IB}} = \frac{{IB}}{{IF}}\) hay IB2 = IA.IF.
c) Ta có: \(\widehat {MAI} = \widehat {AEF}\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung AF)
Vì AE // MB nên \(\widehat {AEF} = \widehat {FMI}\)
Suy ra \(\widehat {MAI} = \widehat {FMI}\)
Xét \(\Delta MAI\) và \(\Delta FMI\) có:
\(\widehat {MAI} = \widehat {FMI}\,\,\left( {cmt} \right)\)
\(\widehat {MIA}\) chung
Do đó \(\Delta MAI\) ᔕ \(\Delta FMI\,\,\left( {g.g} \right)\)
Suy ra \(\frac{{MI}}{{FI}} = \frac{{AI}}{{MI}}\) hay IM2 = IA.IF.
Kết hợp với ý b ta có IB2 = IM2 = IA.IF ⇒ IB = IM (dpcm)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
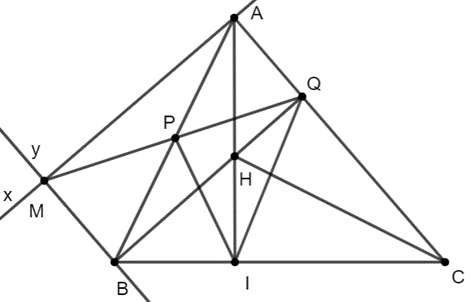
Vì Ax ⊥ AC ⇒ AM ⊥ AC
mà BM // AC
⇒ AM ⊥ BM
Chứng minh tương tự ⇒ AQ // BM và BM // AQ (cmt)
Suy ra AMBQ là hình bình hành.
Mà \(\widehat {AMB} = \widehat {MBQ} = \widehat {ABQ} = \widehat {MAQ} = {90^o}\).
Vậy AMBQ là hình chữ nhật.
b) BQ ⊥ AC (cmt) mà \(BQ \cap AI = H\)
Suy ra H là trực tâm của tam giác ABC.
Do đó: CH ⊥ AB
c) AMBQ là hình chữ nhật mà \(AB \cap QM = P\)
⇒ P là trung điểm AB và P là trung điểm QM
\(\Delta ABI\) vuông tại I có đường trung tuyến IP
⇒ \(IP = \frac{1}{2}AB\)
⇒ IP = PQ
⇒ \(\Delta IPQ\) cân tại P.
Lời giải
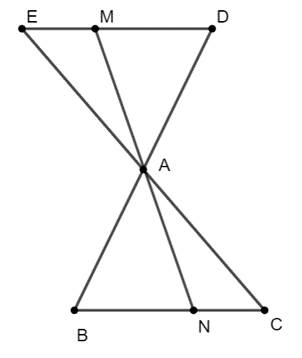
a) Xét \(\Delta ADE\) và \(\Delta ABC\) có:
AD = AB
\(\widehat {DAE} = \widehat {BAC}\) (2 góc đối đỉnh)
AC = AE
⇒ \(\Delta ADE = \Delta BAC\left( {c.g.c} \right)\)
⇒ \(\widehat {ADE} = \widehat {ABC}\) (2 góc tương ứng) mà chúng ở vị trí so le trong với nhau
⇒ BC // DE (đpcm)
b) Xét \(\Delta DAM\) và \(\Delta BAN\) có:
\(\widehat {DAM} = \widehat {BAN}\) (2 góc đối đỉnh)
AD = AB
\(\widehat {ABN} = \widehat {ADM}\) (CMT)
⇒ \(\Delta DAM = \Delta BAN\left( {g.c.g} \right)\)
⇒ AM = AN (2 cạnh tương ứng) (dpcm)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. −8;
B. \(3\sqrt {11} - 13\);
C. −39;
D. −21.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.