Cho nửa đường tròn (O; R) đường kính AB, vẽ hai tiếp tuyến Ax, By với nửa đường tròn. Trên tia Ax lấy điểm E (E khác A, AE < R), trên nửa đường tròn lấy điểm M sao cho EM = EA, đường thẳng EM cắt tia By tại F.
a) Chứng minh EF là tiếp tuyến của đường tròn (O).
b) Chứng minh tam giác EOF là tam giác vuông.
c) Chứng minh AM.OE + BM.OF = AB.EF.
d) Tìm vị trí điểm E trên tia Ax sao cho \({S_{\Delta AMB}} = \frac{3}{4}{S_{\Delta EOF}}\).
Cho nửa đường tròn (O; R) đường kính AB, vẽ hai tiếp tuyến Ax, By với nửa đường tròn. Trên tia Ax lấy điểm E (E khác A, AE < R), trên nửa đường tròn lấy điểm M sao cho EM = EA, đường thẳng EM cắt tia By tại F.
a) Chứng minh EF là tiếp tuyến của đường tròn (O).
b) Chứng minh tam giác EOF là tam giác vuông.
c) Chứng minh AM.OE + BM.OF = AB.EF.
d) Tìm vị trí điểm E trên tia Ax sao cho \({S_{\Delta AMB}} = \frac{3}{4}{S_{\Delta EOF}}\).
Quảng cáo
Trả lời:
Lời giải
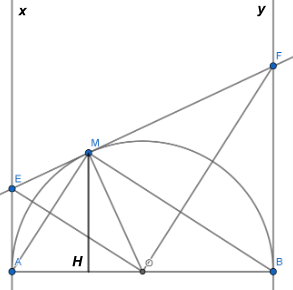
a) Xét ∆AOE và ∆MOE, có:
AO = MO = R;
AE = ME (giả thiết);
OE chung.
Do đó ∆AOE = ∆MOE (c.c.c).
Suy ra \(\widehat {EAO} = \widehat {EMO} = 90^\circ \).
Vậy EF là tiếp tuyến của đường tròn (O).
b) Ta có MF, BF là hai tiếp tuyến của (O).
Suy ra OF là tia phân giác của \(\widehat {MOB}\).
Do đó \(\widehat {MOF} = \widehat {BOF} = \frac{1}{2}\widehat {MOB}\).
Chứng minh tương tự, ta được \(\widehat {AOE} = \widehat {EOM} = \frac{1}{2}\widehat {AOM}\).
Ta có \(\widehat {AOM} + \widehat {MOB} = 180^\circ \) (kề bù).
\( \Rightarrow 2\widehat {EOM} + 2\widehat {MOF} = 180^\circ \).
\( \Rightarrow 2\left( {\widehat {EOM} + \widehat {MOF}} \right) = 180^\circ \).
\( \Rightarrow \widehat {EOF} = 180^\circ :2 = 90^\circ \).
Vậy tam giác EOF vuông tại O.
c) Ta có EA = EM (giả thiết) và OM = OA (= R).
Suy ra OE là đường trung trực của đoạn AM.
Do đó OE ⊥ AM.
Mà MA ⊥ MB (\(\widehat {AMB} = 90^\circ \) do \(\widehat {AMB}\) là góc nội tiếp chắn nửa đường tròn (O)).
Vì vậy OE // MB.
Suy ra \(\widehat {MOE} = \widehat {OMB}\) (so le trong).
Mà \(\widehat {ABM} = \widehat {OMB}\) (do tam giác OMB cân tại O).
Do đó \(\widehat {MOE} = \widehat {ABM}\).
Mà \(\widehat {EMO} = \widehat {AMB} = 90^\circ \).
Vì vậy (g.g).
Suy ra \(\frac{{EM}}{{AM}} = \frac{{OE}}{{AB}}\).
Do đó EM.AB = AM.OE (1)
Chứng minh tương tự, ta được FM.AB = BM.OF (2)
Từ (1), (2), suy ra AM.OE + BM.OF = AB.(EM + FM) = AB.EF.
Vậy ta có điều phải chứng minh.
d) Kẻ MH ⊥ AB tại H.
Ta có \(\widehat {MBA} = \widehat {OFB}\) (cùng phụ với \(\widehat {FOB}\)).
Mà \(\widehat {OFM} = \widehat {OFB}\) (do FO là tia phân giác của \(\widehat {MFB}\)).
Suy ra \(\widehat {MBA} = \widehat {OFE}\).
Mà \(\widehat {AMB} = \widehat {OEF} = 90^\circ \).
Do đó (g.g).
Suy ra \(\frac{{{S_{AMB}}}}{{{S_{EOF}}}} = {\left( {\frac{{MH}}{{OM}}} \right)^2} = \frac{3}{4}\).
Khi đó \(\frac{{MH}}{{OM}} = \frac{{\sqrt 3 }}{2}\).
Vì vậy \(\sin \widehat {MOH} = \frac{{\sqrt 3 }}{2}\).
Suy ra \(\widehat {MOH} = 60^\circ \).
Do đó \(\widehat {MOE} = \widehat {AOE} = 30^\circ \).
Ta có \(AE = OA.\tan \widehat {AOE} = OA.\tan 30^\circ = \frac{{\sqrt 3 }}{3}OA\).
Vậy E nằm trên tia Ax sao cho \(AE = \frac{{\sqrt 3 }}{3}OA\) thỏa mãn yêu cầu bài toán.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
Hàm số đã cho có a = 1 > 0 và \(\frac{{ - b}}{{2a}} = m + 1\) nên hàm số đã cho đồng biến trên khoảng (m + 1; +∞).
Do đó để hàm số đã cho đồng biến trên khoảng (4; 2018) thì (4; 2018) ⊂ (m + 1; +∞).
⇔ m + 1 ≤ 4 ⇔ m ≤ 3.
Mà m là số nguyên dương.
Suy ra m ∈ {1; 2; 3}.
Vậy có 3 giá trị nguyên dương của tham số m thỏa mãn yêu cầu bài toán.
Lời giải
Lời giải
Gọi x là số ha đất trồng ngô, y là số ha đất trồng đậu xanh.
Ta có các điều kiện ràng buộc đối với x, y như sau:
⦁ Hiển nhiên x ≥ 0, y ≥ 0.
⦁ Diện tích canh tác không vượt quá 8 ha nên ta có x + y ≤ 8.
⦁ Số ngày công sử dụng không vượt quá 180 ngày nên 20x + 30y ≤ 180.
⇔ 2x + 3y ≤ 18.
Từ đó, ta có hệ bất phương trình mô tả các điều kiện ràng buộc là:
\(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 8\\2x + 3y \le 18\end{array} \right.\,\,\left( * \right)\).
Yêu cầu bài toán ⇔ Tìm (x; y) thỏa (*) để F(x; y) = 40x + 50y đạt giá trị lớn nhất.
Vẽ và xác định miền nghiệm của (*):
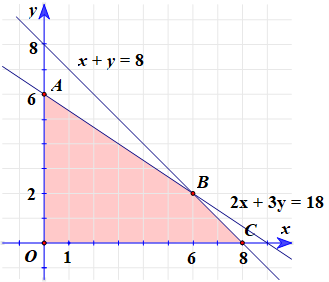
Ta có:
⦁ Miền nghiệm của (*) là tứ giác OABC (kể cả biên).
⦁ O(0; 0), A(0; 6), B(6; 2), C(8; 0).
⦁ F(O) = 0, F(A) = 300, F(B) = 340, F(C) = 320.
Suy ra maxF(x; y) = F(B) = 340 khi và chỉ khi x = 6, y = 2.
Vậy để thu được nhiều tiền nhất thì bác Năm cần trồng 6 ha ngô và 2 ha đậu xanh.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.