Cho tam giác ABC vuông tại A, có AH là đường cao, AM là đường trung tuyến. Qua B kẻ đường thẳng vuông góc với AM tại I cắt AC tại E.
a) Chứng minh BI.BE = 2BH.BM.
b) Chứng minh \(\frac{1}{{A{B^2}}} = \frac{1}{{B{E^2}}} + \frac{1}{{B{C^2}}}\).
Cho tam giác ABC vuông tại A, có AH là đường cao, AM là đường trung tuyến. Qua B kẻ đường thẳng vuông góc với AM tại I cắt AC tại E.
a) Chứng minh BI.BE = 2BH.BM.
b) Chứng minh \(\frac{1}{{A{B^2}}} = \frac{1}{{B{E^2}}} + \frac{1}{{B{C^2}}}\).
Quảng cáo
Trả lời:
Lời giải
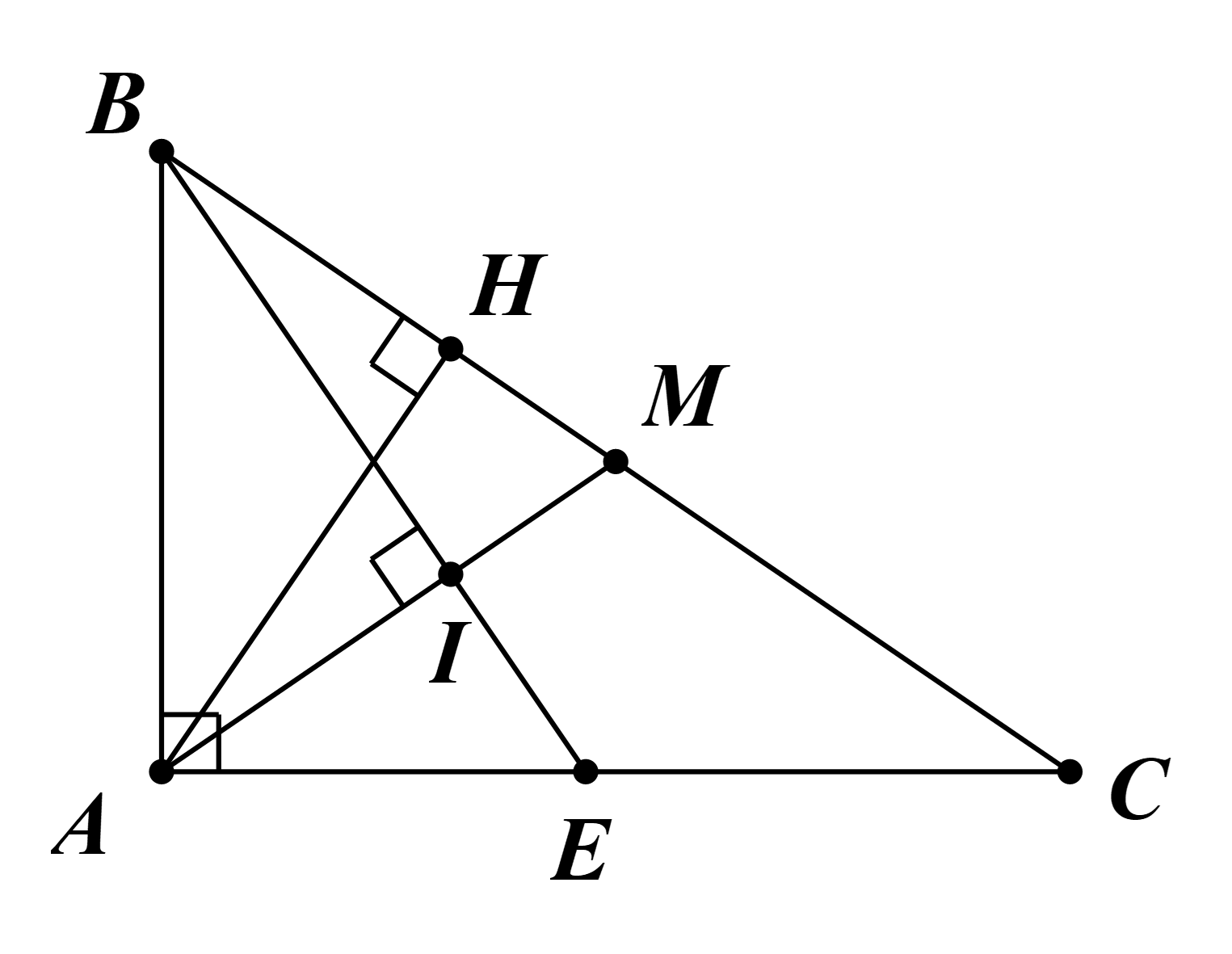
a) Ta có M là trung điểm BC. Suy ra BC = 2BM.
Tam giác ABC vuông tại A có AH là đường cao: AB2 = BH.BC = 2BH.BM (1)
Tam giác ABE vuông tại A có AI là đường cao: AB2 = BI.BE (2)
Từ (1), (2), ta được BI.BE = 2BH.BM.
b) Từ (1), ta có \(BC = \frac{{A{B^2}}}{{BH}}\).
Suy ra \(\frac{1}{{B{C^2}}} = \frac{{B{H^2}}}{{A{B^4}}}\).
Từ (2), ta có \(BE = \frac{{A{B^2}}}{{BI}}\).
Suy ra \(\frac{1}{{B{E^2}}} = \frac{{B{I^2}}}{{A{B^4}}}\).
Xét ∆BMI và ∆AMH, có:
\(\widehat {AMB}\) chung;
\(\widehat {BIM} = \widehat {AHM} = 90^\circ \).
Do đó (g.g).
Suy ra \(\frac{{BI}}{{AH}} = \frac{{BM}}{{AM}}\).
Mà AM = BM (tam giác ABC vuông tại A có AM là đường trung tuyến).
Do đó BI = AH.
Ta có \(\frac{1}{{B{E^2}}} + \frac{1}{{B{C^2}}} = \frac{{B{I^2}}}{{A{B^4}}} + \frac{{B{H^2}}}{{A{B^4}}} = \frac{{B{I^2} + B{H^2}}}{{A{B^4}}} = \frac{{A{H^2} + B{H^2}}}{{A{B^4}}} = \frac{{A{B^2}}}{{A{B^4}}} = \frac{1}{{A{B^2}}}\).
Vậy ta có điều phải chứng minh.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
Hàm số đã cho có a = 1 > 0 và \(\frac{{ - b}}{{2a}} = m + 1\) nên hàm số đã cho đồng biến trên khoảng (m + 1; +∞).
Do đó để hàm số đã cho đồng biến trên khoảng (4; 2018) thì (4; 2018) ⊂ (m + 1; +∞).
⇔ m + 1 ≤ 4 ⇔ m ≤ 3.
Mà m là số nguyên dương.
Suy ra m ∈ {1; 2; 3}.
Vậy có 3 giá trị nguyên dương của tham số m thỏa mãn yêu cầu bài toán.
Lời giải
Lời giải
Gọi x là số ha đất trồng ngô, y là số ha đất trồng đậu xanh.
Ta có các điều kiện ràng buộc đối với x, y như sau:
⦁ Hiển nhiên x ≥ 0, y ≥ 0.
⦁ Diện tích canh tác không vượt quá 8 ha nên ta có x + y ≤ 8.
⦁ Số ngày công sử dụng không vượt quá 180 ngày nên 20x + 30y ≤ 180.
⇔ 2x + 3y ≤ 18.
Từ đó, ta có hệ bất phương trình mô tả các điều kiện ràng buộc là:
\(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 8\\2x + 3y \le 18\end{array} \right.\,\,\left( * \right)\).
Yêu cầu bài toán ⇔ Tìm (x; y) thỏa (*) để F(x; y) = 40x + 50y đạt giá trị lớn nhất.
Vẽ và xác định miền nghiệm của (*):
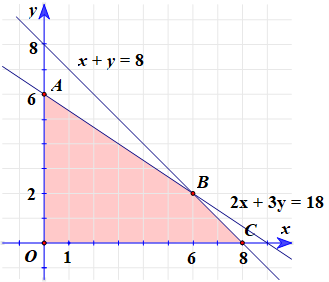
Ta có:
⦁ Miền nghiệm của (*) là tứ giác OABC (kể cả biên).
⦁ O(0; 0), A(0; 6), B(6; 2), C(8; 0).
⦁ F(O) = 0, F(A) = 300, F(B) = 340, F(C) = 320.
Suy ra maxF(x; y) = F(B) = 340 khi và chỉ khi x = 6, y = 2.
Vậy để thu được nhiều tiền nhất thì bác Năm cần trồng 6 ha ngô và 2 ha đậu xanh.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.