Cho hình chóp tam giác đều có thể tích bằng \(32\sqrt 3 {\rm{\;c}}{{\rm{m}}^3}\) và diện tích đáy bằng \(4\sqrt 3 {\rm{\;c}}{{\rm{m}}^2}\). Tính chiều cao của hình chóp tam giác đều đó.
Câu hỏi trong đề: Giải SBT Toán 8 Cánh diều Bài tập cuối chương IV có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
Áp dụng công thức tính thể tích của chóp tam giác đều \(V = \frac{1}{3}.S.h\), S là diện tích đáy, h là chiều cao của hình chóp tam giác đều, V là thể tích.
Do đó ta có: \(32\sqrt 3 = \frac{1}{3}.4\sqrt 3 .h\)
Suy ra h = 24 (cm).
Vậy chiều cao của hình chóp tam giác đều đó là 24 cm.
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
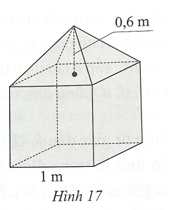
Thể tích phần dưới (có dạng hình lập phương) của khối bê tông là: 13 = 1 (m3).
Thể tích phần trên (có dạng hình chóp tứ giác đều) của khối bê tông là:
\(\frac{1}{3}{.1^2}.0,6 = 0,2\)(m3).
Thể tích của khối bê tông là: 1 + 0,2 = 1,2 (m3).
Đổi 350,55 kg = 0,35055 tấn; 185 lít = 0,185 m3.
Khối lượng xi măng cần dùng để làm khối bê tông đó là:
1,2 . 0,35055 = 0,42066 (tấn).
Lượng nước cần dùng để làm khối bê tông đó là:
1,2 . 0,185 = 0,222 (m3).
Lời giải
Lời giải
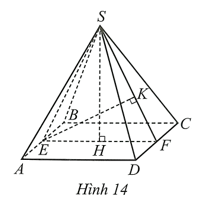
Diện tích của tam giác đều SEF bằng: \(\frac{1}{2}.SH.EF = \frac{1}{2}.EK.SF\) (cm2).
Suy ra SH.EF = EK.SF, mà SH = EK nên SF = EF = 13 cm.
Diện tích xung quanh của hình chóp tứ giác đều S.ABCD là:
\(\frac{1}{2}.\left( {AB.4} \right).SF = \frac{1}{2}.\left( {13.4} \right).13 = 338\) (cm2).
Diện tích đáy của hình chóp tứ giác đều S.ABCD là:
132 = 169 (cm2)
Tổng diện tích các mặt của hình chóp tứ giác đều S.ABCD là:
338 + 169 = 507 (cm2).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập