Giải SBT Toán 8 Cánh diều Bài tập cuối chương IV có đáp án
47 người thi tuần này 4.6 761 lượt thi 12 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bài tập Tính diện tích xung quanh và thể tích của hình chóp tứ giác đều lớp 8 (có lời giải)
Bài tập Tính diện tích xung quanh và thể tích của hình chóp tam giác đều lớp 8 (có lời giải)
Bài tập Các bài toán thực tiễn gắn với việc vận dụng các tam giác vuông đồng dạng lớp 8 (có lời giải)
Bài tập Các bài toán thực tiễn gắn với việc vận dụng định lí Pythagore lớp 8 (có lời giải)
Bài tập Chứng minh các tính chất hình học lớp 8 (có lời giải)
Bài tập Tính độ dài cạnh trong tam giác vuông bằng cách sử dụng định lí Pythagore lớp 8 (có lời giải)
Danh sách câu hỏi:
Lời giải
Lời giải
Đáp án đúng là: D
Thể tích của hình chóp đó là: \(\frac{1}{3}.{a^2}.3a = {a^3}\)(cm3).Lời giải
Lời giải
Đáp án đúng là: C
Áp dụng công thức tính diện tích xung quanh của hình chóp \({S_{xq}} = \frac{1}{2}.C.d\), trong đó C là chu vi đáy, d là độ dài trung đoạn của hình chóp tứ giác đều.
Do đó: \({S_{xq}} = \frac{1}{2}.\left( {3.2x} \right).x = 3{x^2}\) (dm2).
Lời giải
Lời giải
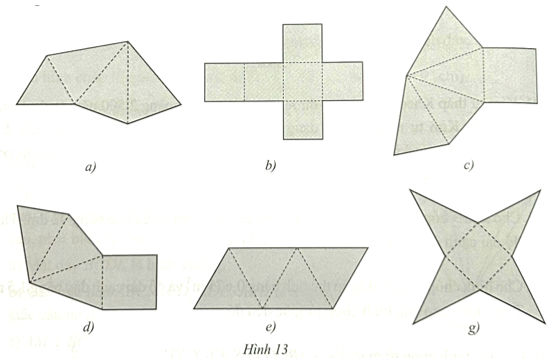
Miếng bìa ở Hình 13a và Hình 13e gấp lại (theo các nét đứt) được hình chóp tam giác đều.
Miếng bìa ở Hình 13c và Hình 13g gấp lại (theo các nét đứt) được hình chóp tứ giác đều.
Miếng bìa ở Hình 13b và Hình \(13d\) không gấp lại (theo các nét đứt) để được hình chóp tam giác đều hoặc hình chóp tứ giác đều.
Lời giải
Lời giải
Các phát biểu a, c, d là đúng.
Phát biểu b là sai vì hình chóp tam giác đều là hình chóp có mặt đáy là tam giác đều.
Lời giải
Lời giải
Áp dụng công thức tính thể tích của chóp tam giác đều \(V = \frac{1}{3}.S.h\), S là diện tích đáy, h là chiều cao của hình chóp tam giác đều, V là thể tích.
Do đó ta có: \(32\sqrt 3 = \frac{1}{3}.4\sqrt 3 .h\)
Suy ra h = 24 (cm).
Vậy chiều cao của hình chóp tam giác đều đó là 24 cm.
Lời giải
Lời giải
Diện tích xung quanh của hình chóp tam giác đều S.ABC là:
\(\frac{1}{2}.\left( {3a} \right).d = \frac{1}{2}.3.2a'.d = 3a'd\) (đơn vị diện tích).
Diện tích xung quanh của hình chóp tam giác đều S’.A’B’C’ là:
\(\frac{1}{2}.\left( {3a'} \right).d' = \frac{3}{2}a'd'\) (đơn vị diện tích).
Do diện tích xung quanh của S.ABC gấp k lần diện tích xung quanh của S’.A’B’C’ nên ta có: \(3a'.d = k.\frac{3}{2}a'.d'\).
Suy ra \(\frac{d}{{d'}} = \frac{k}{2}\).
Vậy tỉ số giữa d và d’ là \(\frac{k}{2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Xem tiếp với tài khoản VIP
Còn 6/12 câu hỏi, đáp án và lời giải chi tiết.
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập