Trong các dãy số (un) được xác định như sau, dãy số giảm là:
A. \({u_n} = \frac{{3n - 1}}{{n + 1}}\).
B. un = n3.
C. \({u_n} = \frac{1}{{{3^{n + 1}}}}\).
D. \({u_n} = \sqrt n \).
Trong các dãy số (un) được xác định như sau, dãy số giảm là:
A. \({u_n} = \frac{{3n - 1}}{{n + 1}}\).
B. un = n3.
C. \({u_n} = \frac{1}{{{3^{n + 1}}}}\).
D. \({u_n} = \sqrt n \).
Câu hỏi trong đề: Giải SBT Toán 11 Cánh Diều Dãy số có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng là: C
Xét đáp án C, ta có:
\({u_{n + 1}} - {u_n} = \frac{1}{{{3^{n + 1 + 1}}}} - \frac{1}{{{3^{n + 1}}}} = \frac{1}{{{3^{n + 2}}}} - \frac{1}{{{3^{n + 1}}}}\)
\( = \frac{{{3^{n + 1}} - {3^{n + 2}}}}{{{3^{n + 1}}{{.3}^{n + 2}}}} = \frac{{{{3.3}^n} - {{9.3}^n}}}{{{3^{n + 1}}{{.3}^{n + 2}}}} = \frac{{ - {{6.3}^n}}}{{{3^{n + 1}}{{.3}^{n + 2}}}} < 0\) với mọi n ∈ ℕ*.
Suy ra un + 1 – un < 0, tức là un + 1 < un.
Vậy dãy số (un) với \({u_n} = \frac{1}{{{3^{n + 1}}}}\) là dãy số giảm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: A
Ta có un + 1 = 3n + 1 = 3n . 31 = 3n . 3.
Lời giải
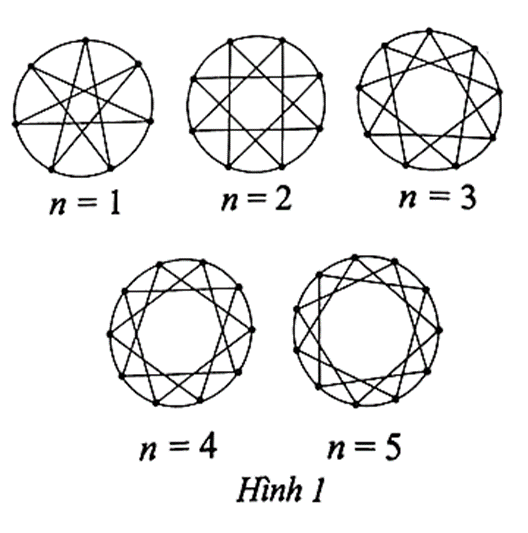
Ta thấy đường tròn được chia thành n + 6 cung bằng nhau và mỗi cung có số đo bằng \(\left( {\frac{{360}}{{n + 6}}} \right)\begin{array}{*{20}{c}}^\circ \\{}\end{array}\). Do mỗi điểm được nối với điểm cách nó hai điểm trên đường tròn nên góc ở đỉnh của mỗi ngôi sao là góc nội tiếp chắn n + 6 – 2 . 3 = n cung bằng nhau đó. Suy ra số đo góc ở đỉnh tính theo đơn vị độ của mỗi ngôi sao là \({u_n} = \frac{1}{2}.\frac{{360}}{{n + 6}}.n = \frac{{180n}}{{n + 6}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.