Quảng cáo
Trả lời:
Giải bởi Vietjack
⦁ Ta xét hình màu đỏ:
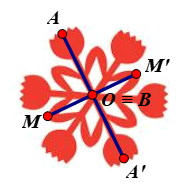
Giả sử ta chọn điểm O trên hình màu đỏ như hình vẽ.
Lấy điểm B trùng O. Khi đó qua O, điểm đối xứng với B là chính nó.
Lấy điểm A bất kì trên hình màu đỏ sao cho A ≠ O.
Khi đó ta luôn xác định được một điểm A’ sao cho O là trung điểm của đoạn AA’.
Tương tự như vậy, với mỗi điểm M bất kì khác O trên hình màu đỏ, ta đều xác định được một điểm M’ trên hình sao cho O là trung điểm của đoạn MM’.
Vậy phép đối xứng tâm O biến hình màu đỏ thành chính nó.
⦁ Ta xét hình màu xanh lá:
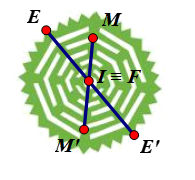
Giả sử ta chọn điểm I trên hình màu xanh lá như hình vẽ.
Lấy điểm F trùng I. Khi đó qua I, điểm đối xứng với F là chính nó.
Lấy điểm E bất kì trên hình màu xanh lá sao cho E ≠ I.
Khi đó ta luôn xác định được một điểm E’ sao cho I là trung điểm của đoạn EE’.
Tương tự như vậy, với mỗi điểm M bất kì khác I trên hình màu xanh lá, ta đều xác định được một điểm M’ trên hình sao cho I là trung điểm của đoạn MM’.
Vậy phép đối xứng tâm I biến hình màu xanh lá thành chính nó.
⦁ Ta xét hình màu xanh biển:
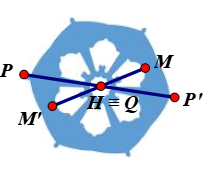
Giả sử ta chọn điểm H trên hình màu xanh biển như hình vẽ.
Lấy điểm P trùng H. Khi đó qua H, điểm đối xứng với P là chính nó.
Lấy điểm P bất kì trên hình màu xanh biển sao cho P ≠ H.
Khi đó ta luôn xác định được một điểm P’ sao cho H là trung điểm của đoạn PP’.
Tương tự như vậy, với mỗi điểm M bất kì khác H trên hình màu xanh biển, ta đều xác định được một điểm M’ trên hình sao cho H là trung điểm của đoạn MM’.
Vậy phép đối xứng tâm H biến hình màu xanh biển thành chính nó.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đường tròn (C): x2 + y2 – 4x – 5 = 0 có tâm I(2; 0), bán kính .
Gọi đường tròn (C’) là ảnh của đường tròn (C) qua phép đối xứng tâm O.
Suy ra đường tròn (C’) có tâm là ảnh của I(2; 0) và bán kính R’ = R = 3.
Gọi I’ = ĐO(I), suy ra O là trung điểm II’ với I(2; 0).
Do đó
Vì vậy tọa độ I’(–2; 0).
Vậy đường tròn (C’) có tâm I’(–2; 0) và bán kính R’ = 3 có phương trình là:
(x + 2)2 + y2 = 9.
Lời giải
a) Gọi M’ là ảnh của M qua ĐO.
Suy ra O là trung điểm của MM’ với M(3; –4).
Do đó
Vậy M’(–3; 4).
b) • Chọn A(0; 2) ∈ d: x – 3y + 6 = 0.
Gọi A’ là ảnh của A qua ĐO.
Suy ra O là trung điểm của AA’ với A(0; 2)
Do đó
Vì vậy A’(0; –2).
• Đường thẳng d: x – 3y + 6 = 0 có vectơ pháp tuyến .
Gọi d’ là ảnh của d qua ĐO.
Suy ra d’ song song hoặc trùng với d, nên d’ nhận vectơ pháp tuyến của d là làm vectơ pháp tuyến.
Vậy đường thẳng d’ đi qua A’(0; –2) và nhận làm vectơ pháp tuyến nên có phương trình là:
1(x – 0) – 3(y + 2) = 0 hay x – 3y – 6 = 0.
c) Đường tròn (C): (x + 2)2 + (y – 1)2 = 4 có tâm I(–2; 1), bán kính R = 2.
Gọi (C’) là ảnh của (C) qua ĐO nên (C’) có tâm là ảnh của I(–2; 1) và có bán kính R’ = R = 2.
Gọi I’ = ĐO(I).
Suy ra O là trung điểm II’.
Do đó
Vì vậy tọa độ I’(2; –1).
Vậy đường tròn (C’) là ảnh của (C) qua ĐO, có tâm I’(2; –1) và R’ = 2 nên có phương trình là:
(x – 2)2 + (y + 1)2 = 4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo