Cho tam giác ABC vuông tại A có đường cao AH biết AC = 20 cm, BH = 9 cm. Tính BC và AH?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
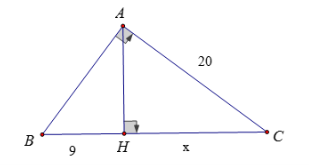
Đặt HC = x (cm)
Xét tam giác ABC vuông tại A có AH ⊥ BC
Theo hệ thức lượng trong tam giác vuông, ta có:
AC2 = CH . BC
\( \Rightarrow {20^2} = \left( {9 + x} \right)x\)
\( \Leftrightarrow {x^2} + 9x - 400 = 0\)
\( \Leftrightarrow \left( {x + 25} \right)\left( {x - 16} \right) = 0\)
\[ \Leftrightarrow \left[ \begin{array}{l}x = - 25\left( {ktm} \right)\\x = 16\end{array} \right.\]
Suy ra BC = BH + CH = 9 + 16 = 25 (cm)
Xét tam giác ABC vuông tại A có AH ⊥ BC
Theo hệ thức lượng trong tam giác vuông, ta có:
AH2 = CH . BH = 9 . 16 = 144
Suy ra AH = 12 (cm)
Vậy BC = 25 cm, AH = 12 cm.
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(m = \frac{3}{4}\);
B. \(m = \frac{3}{2}\);
C. \(m = \frac{1}{4}\);
D. \(m = - \frac{1}{2}\).
Lời giải
Lời giải
Đáp án đúng là: A
Tập xác định D = ℝ
Ta có:
\(y' = 3{x^2} - 6x = 0\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0 \Rightarrow y = 1}\\{x = 2 \Rightarrow y = - 3}\end{array}} \right.\)
Suy ra A(0; 1) và B(2; –3) là hai điểm cực trị của đồ thị hàm số y = x3 – 3x2 + 1
Phương trình đường thẳng đi qua hai điểm cực trị trên là
\(\frac{{x - 0}}{{2 - 0}} = \frac{{y - 1}}{{ - 3 - 1}}\)
⇔ –2x = y – 1
⇔ y = –2x + 1 (d’)
Vì d ⊥ d’ nên \(\left( {2m - 1} \right).\left( { - 2} \right) = - 1 \Leftrightarrow 2m - 1 = \frac{1}{2} \Leftrightarrow m = \frac{3}{4}\)
Vậy ta chọn đáp án A.
Lời giải
Lời giải
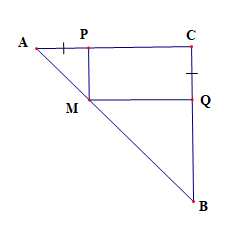
Vì tam giác ABC vuông cân tại C
Nên AC = BC, \(\widehat {CAB} = \widehat {CBA} = 45^\circ \)
Ta có PM // BC và AC ⊥ CB
Suy ra PM ⊥ AC
Do đó tam giác APM vuông tại P
Lại có \(\widehat {PAM} = 45^\circ \)
Suy ra \(\widehat {PAM} = \widehat {PMA} = 45^\circ \)
Do đó tam giác APM vuông cân tại P
Suy ra PA = PM
Mà PA = CQ (giả thiết)
Suy ra PM = CQ
Xét tứ giác PCQM có
PM = CQ
Mà PM // CQ
Suy ra PCQM là hình bình hành
Lại có: \(\widehat C = 90^\circ \)
Suy ra PCQM là hình chữ nhật
Vậy PCQM là hình chữ nhật.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(\frac{5}{9}\);
B. \(\frac{5}{{36}}\);
C. \(\frac{5}{{18}}\);
D. \(\frac{5}{{72}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. δ ≤ 0,0000099
B. δ ≤ 0,000039
C. δ ≤ 0,0000039
D. δ < 0,000039.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo