7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án (Phần 40)
53 người thi tuần này 4.6 86.9 K lượt thi 46 câu hỏi 50 phút
🔥 Đề thi HOT:
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
84.5 K lượt thi
126 câu hỏi
237 câu Bài tập Hàm số mũ, logarit ôn thi Đại học có lời giải (P1)
31.2 K lượt thi
30 câu hỏi
240 câu Bài tập Hàm số mũ, logarit ôn thi THPT Quốc gia có lời giải (P1)
25.3 K lượt thi
30 câu hỏi
10000 câu trắc nghiệm tổng hợp môn Toán 2025 mới nhất (có đáp án) - Phần 1
12.7 K lượt thi
500 câu hỏi
7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 1)
89.4 K lượt thi
304 câu hỏi
62 câu Trắc nghiệm Khái niệm về khối đa diện (nhận biết)
18.7 K lượt thi
19 câu hỏi
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
20 K lượt thi
20 câu hỏi
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
16.9 K lượt thi
40 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
Lời giải
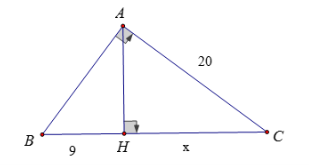
Đặt HC = x (cm)
Xét tam giác ABC vuông tại A có AH ⊥ BC
Theo hệ thức lượng trong tam giác vuông, ta có:
AC2 = CH . BC
\( \Rightarrow {20^2} = \left( {9 + x} \right)x\)
\( \Leftrightarrow {x^2} + 9x - 400 = 0\)
\( \Leftrightarrow \left( {x + 25} \right)\left( {x - 16} \right) = 0\)
\[ \Leftrightarrow \left[ \begin{array}{l}x = - 25\left( {ktm} \right)\\x = 16\end{array} \right.\]
Suy ra BC = BH + CH = 9 + 16 = 25 (cm)
Xét tam giác ABC vuông tại A có AH ⊥ BC
Theo hệ thức lượng trong tam giác vuông, ta có:
AH2 = CH . BH = 9 . 16 = 144
Suy ra AH = 12 (cm)
Vậy BC = 25 cm, AH = 12 cm.
Lời giải
Lời giải
Hoành độ giao điểm của (P) và (d) là nghiệm của phương trình:
x2 – 3x + 2 = x + m
⇔ x2 – 4x + 2 – m = 0
Ta có: ∆’ = (–2)2 – (2 – m) = m + 2
Để d) và (P) cắt nhau tại hai điểm phân biệt thì ∆’ > 0
\( \Leftrightarrow m + 2 > 0\)
\( \Leftrightarrow m > - 2\)
Vậy m > –2 thì (d) và (P) cắt nhau tại hai điểm phân biệt.
Câu 3
A. (– ∞; 1)
B. [1; +∞)
C. [–1; 1]
D. (– ∞; –1].
Lời giải
Lời giải
Đáp án đúng là: D
Hàm số \(y = \sqrt {{x^2} + 1} - m{\rm{x}} - 1\)
\(y' = \frac{x}{{\sqrt {{x^2} + 1} }} - m\)
Hàm số luôn đồng biến khi và chỉ khi \(m \le \frac{x}{{\sqrt {{x^2} + 1} }}\)
Xét hàm số \(f\left( x \right) = \frac{x}{{\sqrt {{x^2} + 1} }};f'\left( x \right) = \frac{1}{{\sqrt {{{\left( {{x^2} + 1} \right)}^3}} }} > 0,\forall x\)
Suy ra f(x) luôn đồng biến trên ℝ
Mặt khác \(\mathop {\lim }\limits_{x \to - \infty } \frac{x}{{\sqrt {{x^2} + 1} }} = - 1\)
Suy ra m ≤ –1
Vậy ta chọn đáp án D.
Lời giải
Lời giải
Để đường thẳng (d) song song với đường thẳng y = 2x + 5 thì
\(\left\{ \begin{array}{l}2m--1 = 2\\3 - m \ne 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = \frac{3}{2}\\m \ne - 2\end{array} \right. \Leftrightarrow m = \frac{3}{2}\)
Vậy \(m = \frac{3}{2}\).
Câu 5
A. \(m = \frac{3}{4}\);
B. \(m = \frac{3}{2}\);
C. \(m = \frac{1}{4}\);
D. \(m = - \frac{1}{2}\).
Lời giải
Lời giải
Đáp án đúng là: A
Tập xác định D = ℝ
Ta có:
\(y' = 3{x^2} - 6x = 0\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0 \Rightarrow y = 1}\\{x = 2 \Rightarrow y = - 3}\end{array}} \right.\)
Suy ra A(0; 1) và B(2; –3) là hai điểm cực trị của đồ thị hàm số y = x3 – 3x2 + 1
Phương trình đường thẳng đi qua hai điểm cực trị trên là
\(\frac{{x - 0}}{{2 - 0}} = \frac{{y - 1}}{{ - 3 - 1}}\)
⇔ –2x = y – 1
⇔ y = –2x + 1 (d’)
Vì d ⊥ d’ nên \(\left( {2m - 1} \right).\left( { - 2} \right) = - 1 \Leftrightarrow 2m - 1 = \frac{1}{2} \Leftrightarrow m = \frac{3}{4}\)
Vậy ta chọn đáp án A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. –2 < m < 5
B. m > –3
C. –1 < m < 5
D. 1 < m < 5.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. Đường thẳng đi qua trung điểm hai cạnh bên của hình thang cân.
B. Đường chéo của hình thang cân.
C. Đường thẳng vuông góc với hai đáy của hình thang cân.
D. Đường thẳng đi qua trung điểm hai đáy của hình thang cân.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
A. \(2 \le m \le \frac{{21 + 2\sqrt {34} }}{{10}}\)
B. \(m \le \frac{{21 + 2\sqrt {34} }}{{10}}\)
C. m ≥ 2
D. \(\left[ \begin{array}{l}m < 2\\m > \frac{{21 + 2\sqrt {34} }}{{10}}\end{array} \right.\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
A. A, B, C;
B. B, C, D;
C. A, B, D;
D. A, C, D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 22
A. Đường thẳng d trùng với HA
B. Đường thẳng d tạo với HA một góc 45°
C. Đường thẳng d tạo với HA một góc 60°
D. Đường thẳng d vuông góc với HA.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 28
A. x2 + (y – 11)2 = 11
B. x2 + (y + 11)2 = 121
C. x2 + (y – 11)2 = 121
D. x2 + (y + 11)2 = 11.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 32
A. \(\frac{5}{9}\);
B. \(\frac{5}{{36}}\);
C. \(\frac{5}{{18}}\);
D. \(\frac{5}{{72}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 33
A. \(\left[ \begin{array}{l}m = - 4\\m = 2\end{array} \right.\);
B. \(\left[ \begin{array}{l}m = - 4\\m = - 2\end{array} \right.\);
C. \(\left[ \begin{array}{l}m = 4\\m = 2\end{array} \right.\);
D. \(\left[ \begin{array}{l}m = 4\\m = - 2\end{array} \right.\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 38
A. 3310
B. 2130
C. 3210
D. 3320.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 39
A. L = 32,376 ± 0,025 và ∆L ≤ 0,05
B. L = 32,376 ± 0,05 và ∆L ≤ 0,025
C. L = 32,376 ± 0,5 và ∆L ≤ 0,5
D. L = 32,376 ± 0,05 và ∆L ≤ 0,05.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 43
A. a = –1, a = 3
B. a = 2
C. a = 1, a = –3
D. Không tồn tại giá trị của a.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 46
A. δ ≤ 0,0000099
B. δ ≤ 0,000039
C. δ ≤ 0,0000039
D. δ < 0,000039.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo