7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án (Phần 54)

🔥 Đề thi HOT:

1171 người thi tuần này

7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 1)

69.5 K lượt thi 304 câu hỏi

886 người thi tuần này

20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)

11.3 K lượt thi 20 câu hỏi

870 người thi tuần này

5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)

67.5 K lượt thi 126 câu hỏi

800 người thi tuần này

124 câu Trắc nghiệm Ôn tập Toán 12 Chương 3 Hình học có đáp án (Phần 1)

13.1 K lượt thi 25 câu hỏi

739 người thi tuần này

7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)

10.1 K lượt thi 7 câu hỏi

738 người thi tuần này

15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)

10.9 K lượt thi 15 câu hỏi

723 người thi tuần này

62 câu Trắc nghiệm Khái niệm về khối đa diện (nhận biết)

12.6 K lượt thi 19 câu hỏi

686 người thi tuần này

56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án

9.9 K lượt thi 56 câu hỏi

Nội dung liên quan:

237 câu Bài tập Hàm số mũ, logarit ôn thi Đại học có lời giải

lượt thi

8 đề

240 câu Bài tập Hàm số mũ, logarit ôn thi THPT Quốc gia có lời giải

lượt thi

8 đề

215 câu Bài tập Hàm số mũ, logarit cơ bản, nâng cao có lời giải

lượt thi

7 đề

175 câu Bài tập Số phức cơ bản, nâng cao có lời giải

lượt thi

7 đề

225 Bài tập Số phức ôn thi Đại học có lời giải

lượt thi

8 đề

250 câu Bài tập Tích phân ôn thi Đại học có lời giải

lượt thi

10 đề

213 câu Bài tập Tích phân cơ bản, nâng cao có lời giải

lượt thi

9 đề

299 Bài trắc nghiệm hàm số mũ, hàm số Logarit siêu hay có lời giải chi tiết

lượt thi

8 đề

255 Bài trắc nghiệm Hàm số mũ và Logarit cơ bản nâng cao cực hay có lời giải

lượt thi

7 đề

71 Bài trắc nghiệm Khối đa diện trong đề thi Đại học cực hay có lời giải

lượt thi

3 đề

Danh sách câu hỏi:

Câu 1

Cho hàm số f(x) có bảng biến thiên như sau

Có bao nhiêu giá trị nguyên của tham số m để phương trình 3f(x² – 4x) = m có ít nhất ba nghiệm thực phân biệt thuộc khoảng (0; +∞)?

A. 15

B. 14

C. 13

D. 12.

Lời giải

Đáp án đúng là: A

Phương trình: 3f(x² – 4x) = m (1)

Đặt u = x² – 4x

Ta có bảng biến thiên sau

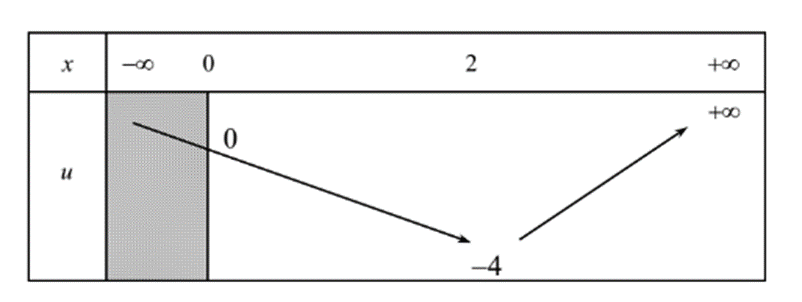
Có bao nhiêu giá trị nguyên của tham số m để phương trình 3f(x^2 - 4x) = m có ít nhất (ảnh 2)

Ta thấy:

+) Với u < –4, phương trình (1) vô nghiệm

+) Với u = –4, phương trình (1) có một nghiệm x = 2 > 0

+) Với –4 < u < 0, phương trình (1) có hai nghiệm x > 0

+) Với u ≥ 0, phương trình (1) có một nghiệm x > 0

Khi đó 3f(x² – 4x) = m

\( \Rightarrow f\left( u \right) = \frac{m}{3}\) (2)

Ta thấy:

+) Nếu \(\frac{m}{3} = - 3 \Leftrightarrow m = - 9\) thì phương trình (2) có một nghiệm u = 0

Nên phương trình (1) có một nghiệm x > 0

+) Nếu \( - 3 < \frac{m}{3} < - 2 \Leftrightarrow - 9 < m < - 6\) thì phương trình (2) có một nghiệm u > 0 và một nghiệm u ∈ (–2; 0)

Nên phương trình (1) có ba nghiệm x > 0

+) Nếu \(\frac{m}{3} = - 2 \Leftrightarrow m = - 6\) thì phương trình (2) có một nghiệm u = –4, một nghiệm u ∈ (–2; 0) và một nghiệm u > 0

Nên phương trình (1) có bốn nghiệm x > 0

+) Nếu \( - 2 < \frac{m}{3} < 2 \Leftrightarrow - 6 < m < 6\) thì phương trình (2) có một nghiệm u < –4, hai nghiệm u ∈ (–4; 0) và một nghiệm u > 0

Nên phương trình (1) có năm nghiệm x > 0

+) Nếu \(\frac{m}{3} = 2 \Leftrightarrow m = 6\) thì phương trình (2) có một nghiệm u < –4, một nghiệm u = –2 và một nghiệm u > 0

Nên phương trình (1) có ba nghiệm x > 0

+) Nếu \(\frac{m}{3} > 2 \Leftrightarrow m > 6\) thì phương trình (2) có một nghiệm u < –4 và một nghiệm u > 0

Nên phương trình (1) có một nghiệm x > 0

Suy ra –9 < m ≤ 6

Do đó m ∈ {–8; –7; –6; –5; –4; –3; –2; –1; 0; 1; 2; 3; 4; 5; 6}

Vậy ta chọn đáp án A.

Câu 2

Tìm m để \(y = \frac{{{x^2} + m{\rm{x}}}}{{1 - x}}\) có cực trị và khoảng cách giữa 2 điểm cực trị bằng 10.

Xem đáp án

Lời giải

\(y' = \frac{{ - \left( {{x^2} - 2{\rm{x}} - m} \right)}}{{{{\left( {1 - x} \right)}^2}}}\)

Để hàm số \(y = \frac{{{x^2} + m{\rm{x}}}}{{1 - x}}\) có 2 cực trị

⇔ y’ = 0 có hai nghiệm phân biệt

⇔ x² – 2x – m = 0 có hai nghiệm phân biệt

Điều kiện \(\left\{ \begin{array}{l}f\left( 1 \right) = - 1 - m \ne 0\\\Delta ' = 1 + m > 0\end{array} \right. \Leftrightarrow m > - 1\)

Theo định lý Vi – ét, hai nghiệm của phương trình thỏa mãn

\(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\\{x_1}.{x_2} = - m\end{array} \right.{\rm{ }}(1)\)

Khoảng cách giữa hai điểm cực trị là

\({d^2} = {\left( {{{\rm{x}}_1} - {x_2}} \right)^2} + {\left( {{y_1} - {y_2}} \right)^2} = {\left( {{{\rm{x}}_1} - {x_2}} \right)^2} + {\left( { - {x_1} + \frac{{m + 1}}{{1 - {x_1}}} + {x_2} - \frac{{m + 1}}{{1 - {x_2}}}} \right)^2} = 100\)

\( \Leftrightarrow {x_1}^2 - 2{{\rm{x}}_1}{x_2} + {x_2}^2 + {\left( {{x_2} - {x_1} + \frac{{\left( {m + 1} \right)\left( {1 - {x_2}} \right) - \left( {m + 1} \right)\left( {1 - {x_1}} \right)}}{{\left( {1 - {x_1}} \right)\left( {1 - {x_2}} \right)}}} \right)^2} = 100\)

\( \Leftrightarrow \left( {{x_1}^2 + 2{{\rm{x}}_1}{x_2} + {x_2}^2} \right) - 4{{\rm{x}}_1}{x_2} + {\left( {{x_2} - {x_1} + \frac{{m - m{{\rm{x}}_2} + 1 - {x_2} - m + m{{\rm{x}}_1} - 1 + {x_1}}}{{\left( {1 - {x_1}} \right)\left( {1 - {x_2}} \right)}}} \right)^2} = 100\)

\( \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 4{{\rm{x}}_1}{x_2} + {\left( {{x_2} - {x_1} + \frac{{ - m{{\rm{x}}_2} - {x_2} + m{{\rm{x}}_1} + {x_1}}}{{1 - {x_1} - {x_2} + {x_1}{x_2}}}} \right)^2} = 100\)

\( \Leftrightarrow {2^2} - 4.\left( { - m} \right) + {\left( {{x_2} - {x_1} + \frac{{ - m{{\rm{x}}_2} - {x_2} + m{{\rm{x}}_1} + {x_1}}}{{1 - 2 - m}}} \right)^2} = 100\)

\( \Leftrightarrow 4 + 4m + {\left( {{x_2} - {x_1} + \frac{{ - m{{\rm{x}}_2} - {x_2} + m{{\rm{x}}_1} + {x_1}}}{{ - 1 - m}}} \right)^2} = 100\)

\( \Leftrightarrow 4 + 4m + {\left( {\frac{{\left( {{x_2} - {x_1}} \right)\left( { - 1 - m} \right) - m{{\rm{x}}_2} - {x_2} + m{{\rm{x}}_1} + {x_1}}}{{ - 1 - m}}} \right)^2} = 100\)

\( \Leftrightarrow 4 + 4m + {\left( {\frac{{ - {x_2} - m{{\rm{x}}_2} + {x_1} + m{{\rm{x}}_1} - m{{\rm{x}}_2} - {x_2} + m{{\rm{x}}_1} + {x_1}}}{{ - 1 - m}}} \right)^2} = 100\)

\( \Leftrightarrow 4 + 4m + {\left( {\frac{{2{x_2} + 2m{{\rm{x}}_2} - 2{x_1} - 2m{{\rm{x}}_1}}}{{1 + m}}} \right)^2} = 100\)

\( \Leftrightarrow 4 + 4m + 4{\left( {\frac{{\left( {{x_2} - {x_1}} \right)\left( {1 + m} \right)}}{{1 + m}}} \right)^2} = 100\)

\( \Leftrightarrow 4 + 4m + 4{\left( {{x_2} - {x_1}} \right)^2} = 100\)

\( \Leftrightarrow 4 + 4m + 4\left[ {{{\left( {{x_2} + {x_1}} \right)}^2} - 2{{\rm{x}}_1}{x_2}} \right] = 100\)

\( \Leftrightarrow 4 + 4m + 4\left( {4 + 4m} \right) = 100\)

\( \Leftrightarrow 20m + 20 = 100\)

\( \Leftrightarrow 20m = 80\)

\( \Leftrightarrow m = 4\)

Vậy m = 4.

Câu 3

Phân tích đa thức thành nhân tử (x + y)³ – ( x – y)³.

Xem đáp án

Lời giải

Ta có:

\(\begin{array}{l}{(x + y)^3} - {(x - y)^3}\\ = {x^3} + 3{x^2}y + 3x{y^2} + {y^3} - {x^3} + 3{x^2}y - 3x{y^2} + {y^3}\\ = 6{x^2}y + 2{y^3}\\ = 2y\left( {3{x^2} + {y^2}} \right).\end{array}\)

Câu 4

Phân tích đa thức sau thành nhân tử: x² + 6x + 9.

Xem đáp án

Lời giải

Ta có:

x² + 6x + 9

= x² + 2 . 3 . x + 3²

= (x + 3)².

Câu 5

Cho \(A = \frac{1}{{2 + 2\sqrt a }} + \frac{1}{{2 - 2\sqrt a }} - \frac{{{a^2} + 1}}{{1 - {a^2}}}\)

a) Tìm điều kiện xác định rồi rút gọn A

b) Tìm a để \[{\rm{A}} < \frac{1}{3}\].

Xem đáp án

Lời giải

a) Điều kiện xác định a ≥ 0, a ≠ 1

\(A = \frac{1}{{2 + 2\sqrt a }} + \frac{1}{{2 - 2\sqrt a }} - \frac{{{a^2} + 1}}{{1 - {a^2}}}\)

\({\rm{A}} = \frac{1}{{2\left( {1 + \sqrt a } \right)}} + \frac{1}{{2\left( {1 - \sqrt a } \right)}} - \frac{{{a^2} + 1}}{{\left( {1 - a} \right)\left( {1 + a} \right)}}\)

\({\rm{A}} = \frac{1}{{2\left( {1 + \sqrt a } \right)}} + \frac{1}{{2\left( {1 - \sqrt a } \right)}} - \frac{{{a^2} + 1}}{{\left( {1 - \sqrt a } \right)\left( {1 + \sqrt a } \right)\left( {1 + a} \right)}}\)

\(A = \frac{{\left( {1 - \sqrt a } \right)\left( {1 + a} \right) + \left( {1 + \sqrt a } \right)\left( {1 + a} \right) - \left( {{a^2} + 1} \right)2}}{{2\left( {1 + \sqrt a } \right)\left( {1 - \sqrt a } \right)\left( {1 + a} \right)}}\)

\(A = \frac{{1 + a - \sqrt a - a\sqrt a + 1 + a + \sqrt a + a\sqrt a - 2{a^2} + 2}}{{2\left( {1 + \sqrt a } \right)\left( {1 - \sqrt a } \right)\left( {1 + a} \right)}}\)

\({\rm{A}} = \frac{{2a - 2{a^2}}}{{2\left( {1 - a} \right)\left( {1 + a} \right)}}\)

\({\rm{A}} = \frac{{2a\left( {1 - a} \right)}}{{2\left( {1 - a} \right)\left( {1 + a} \right)}}\)

\({\rm{A}} = \frac{a}{{1 + a}}\)

b) Để \[{\rm{A}} < \frac{1}{3}\]\( \Leftrightarrow \frac{a}{{1 + a}} < \frac{1}{3}\)

\( \Leftrightarrow \frac{a}{{1 + a}} - \frac{1}{3} < 0\)\( \Leftrightarrow \frac{{3a - a - 1}}{{1 + a}} < 0\)

\( \Leftrightarrow 2{\rm{a}} - 1 < 0\)\( \Leftrightarrow {\rm{a}} < \frac{1}{2}\)

Mà a ≥ 0, a ≠ 1

Suy ra \({\rm{0}} \le {\rm{a}} < \frac{1}{2}\)

Vậy \({\rm{0}} \le {\rm{a}} < \frac{1}{2}\).

Câu 6

Trong mặt phẳng tọa độ Oxy, phương trình đường tròn (C') là ảnh của đường tròn qua (C): x² + y² – 2x + 4y – 1 = 0 với \(\overrightarrow v = \left( {1;2} \right)\) là:

A. \({\left( {x + 2} \right)^2} + {y^2} = \sqrt 6 \)

B. \({\left( {x - 2} \right)^2} + {y^2} = 6\)

C. x² + y² – 2x – 5 = 0

D. 2x² + 2y² – 8x + 4 = 0.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án (Phần 54)

🔥 Đề thi HOT:

7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 1)

20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)

5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)

124 câu Trắc nghiệm Ôn tập Toán 12 Chương 3 Hình học có đáp án (Phần 1)

7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)

15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)

62 câu Trắc nghiệm Khái niệm về khối đa diện (nhận biết)

56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án

Nội dung liên quan:

237 câu Bài tập Hàm số mũ, logarit ôn thi Đại học có lời giải

240 câu Bài tập Hàm số mũ, logarit ôn thi THPT Quốc gia có lời giải

215 câu Bài tập Hàm số mũ, logarit cơ bản, nâng cao có lời giải

175 câu Bài tập Số phức cơ bản, nâng cao có lời giải

225 Bài tập Số phức ôn thi Đại học có lời giải

250 câu Bài tập Tích phân ôn thi Đại học có lời giải

213 câu Bài tập Tích phân cơ bản, nâng cao có lời giải

299 Bài trắc nghiệm hàm số mũ, hàm số Logarit siêu hay có lời giải chi tiết

255 Bài trắc nghiệm Hàm số mũ và Logarit cơ bản nâng cao cực hay có lời giải

71 Bài trắc nghiệm Khối đa diện trong đề thi Đại học cực hay có lời giải

Danh sách câu hỏi:

Cho hàm số f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của tham số m để phương trình 3f(x2 – 4x) = m có ít nhất ba nghiệm thực phân biệt thuộc khoảng (0; +∞)?

Tìm m để \(y = \frac{{{x^2} + m{\rm{x}}}}{{1 - x}}\) có cực trị và khoảng cách giữa 2 điểm cực trị bằng 10.

Phân tích đa thức thành nhân tử (x + y)3 – ( x – y)3.

Phân tích đa thức sau thành nhân tử: x2 + 6x + 9.

Cho \(A = \frac{1}{{2 + 2\sqrt a }} + \frac{1}{{2 - 2\sqrt a }} - \frac{{{a^2} + 1}}{{1 - {a^2}}}\) a) Tìm điều kiện xác định rồi rút gọn A b) Tìm a để \[{\rm{A}} < \frac{1}{3}\].

Trong mặt phẳng tọa độ Oxy, phương trình đường tròn (C') là ảnh của đường tròn qua (C): x2 + y2 – 2x + 4y – 1 = 0 với \(\overrightarrow v = \left( {1;2} \right)\) là:

Tìm giá trị nhỏ nhất của hàm số \(y = 3{\rm{x}} + \frac{4}{{{x^2}}}\) trên khoảng (0; +∞).

Cho hàm số \((C):y = \frac{{x + 2}}{{x - 1}}\) Cho điểm M(0; m). Xác định m để từ A kẻ được 2 tiếp tuyến đến (C) sao cho 2 tiếp tuyến tương ứng nằm về hai phía đối với trục Ox.

Tìm các số nguyên x, y thỏa mãn x3 + 2x2 + 3x + 2 = y3.

Tập xác định của hàm số y = logx là:

Cho các số dương x, y, z thỏa mãn điều kiện xy + yz + zx = xyz. Chứng minh rằng: \(\sqrt {x + yz} + \sqrt {y + x{\rm{z}}} + \sqrt {z + xy} \ge \sqrt {xyz} + \sqrt x + \sqrt y + \sqrt z \).

Giải hệ phương trình \(\left\{ \begin{array}{l}y + x{y^2} = 6{{\rm{x}}^2}\\1 + {x^2}{y^2} = 5{{\rm{x}}^2}\end{array} \right.\).

Đạo hàm của hàm số y = log(1 – x) bằng:

Cho x, y là các số thực dương và m, n là hai số thực tùy ý. Đẳng thức nào sau đây là sai?

Hình bình hành ABCD có AC ⊥ AD và AD = 3,5; \(\widehat D = 50^\circ \). Tính diện tích ABCD.

Tìm tất cả các giá trị của tham số m để hàm số y = x3 + x2 + mx + 1 đồng biến trên khoảng (–∞; +∞)

Chứng minh bất đẳng thức sinx < x với mọi x > 0 và sinx > x với mọi x < 0.

Cho hàm số y = – x3 + 3x2 + 3mx – 1, tìm tất cả các giá trị của tham số m để hàm số nghịch biến trên khoảng (0; +∞)

Tính tổng: S = 12 + 22 + 32 + ... + n2.

Cho tam giác ABC có cạnh a, b, c thỏa mãn bc = a2. Chứng minh rằng sinB.sinC = sin2A và hb . hc = ha2.

Cho tam giác ABC có cạnh a, b, c thỏa mãn bc = a2.

Chứng minh rằng sinB.sinC = sin2A và hb . hc = ha2.

Cho 4 chữ số 1, 5, 8, 9 có thể viết được mấy số có 4 chữ số khác nhau từ các chữ số trên.

Tìm x biết x² – 9 + 5(x – 3) = 0.

Thực hiện phép tính: (102 + 112 + 122) : (132 + 142).

Tìm x biết (8x – 7)(8x – 5)(2x – 1)(4x – 1) = 9.

Trong các mệnh đề sau, mệnh đề nào đúng?

Tính \(\frac{{{x^6} - {y^6}}}{{{x^4} - {y^4} - {x^3}y + x{y^3}}}\).

Cho a là số thực dương, a ≠ 1 và \(P = {\log _{\sqrt[3]{a}}}{a^3}\). Mệnh đề nào dưới đây đúng?

Phân tích đa thức thành nhân tử: (x – 1)(x – 2)(x + 7)(x + 8) + 8.

Khai triển (x – 2)2.

Chứng minh với ab ≥ 1 thì \(\frac{1}{{1 + {a^2}}} + \frac{1}{{1 + {b^2}}} \ge \frac{2}{{1 + ab}}\).

Cho a, b, c là 3 cạnh trong tam giác. Chứng minh rằng: \(\frac{a}{{b + c - a}} + \frac{b}{{a + c - b}} + \frac{c}{{a + b - c}} \ge 3\).

Cho ngũ giác ABCDE. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DE. Gọi I và J lần lượt là trung điểm của MP và NQ. Chứng minh IJ song song với AE và \[{\rm{IJ}} = \frac{1}{4}A{\rm{E}}\].

Cho tam giác ABC vuông tại A, đường cao AH. Chứng minh: a) AB2 = BH . BC b) AC2 = CH . BC c) \(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}\).

Chứng minh với x, y, z dương ta có \(\frac{{{x^3}}}{{yz}} + \frac{{{y^3}}}{{xz}} + \frac{{{z^3}}}{{xy}} \ge x + y + z\).

Với a, b, c là các số dương, chứng minh rằng \(\left( {a + b + c} \right)\left( {\frac{1}{a} + \frac{1}{b} + \frac{1}{c}} \right) \ge 9\).

Tìm giá trị nhỏ nhất của x2 + 3x + 4.

Cho hàm số f(x) có bảng xét dấu của đạo hàm như sau: Hàm số y = 3f(x + 2) – x3 + 3x đồng biến trên khoảng nào dưới đây?

Tổng các nghiệm của phương trình 3x+1 + 31-x = 10.

Rút gọn các phân thức sau: a) \(\frac{{{y^3} - {x^3}}}{{{x^3} - 3{{\rm{x}}^2}y + 3{\rm{x}}{y^2} - {y^3}}}\) b) \(\frac{{{x^5} + x + 1}}{{{x^3} + {x^2} + x}}\) c) \(\frac{{2{{\rm{x}}^2} - x - 3}}{{{x^2} - 4x - 5}}\).

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của SA, SB. a) Tìm giao tuyến của (SAC) và (SBD) b) Tìm giao điểm DN với (SAC) c) Chứng minh MN // (SCD).

Mệnh đề nào sau đây đúng ?

Phân tích đa thức sau thành nhân tử bằng phương pháp nhóm hạng tử: x2 – 2x – 4y2 – 4y.

Phân tích đa thức thành nhân tử: x3 – 7x – 6.

Chứng minh \(\frac{1}{{1 + {a^3}}} + \frac{1}{{1 + {b^3}}} + \frac{1}{{1 + {c^3}}} \ge \frac{3}{{1 + abc}}\) với a, b, c ≥ 1.

Cho A = 5n+2 + 26 . 5n + 82n + 1. Chứng minh A ⋮ 59.

Cho x > 0, y > 0 và x + y = 1. Chứng minh: \(8\left( {{x^4} + {y^4}} \right) + \frac{1}{{xy}} \ge 5\).

Chứng minh rằng a4 + b4 + c4 ≥ abc(a + b + c).

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho hàm số f(x) có bảng biến thiên như sau

Có bao nhiêu giá trị nguyên của tham số m để phương trình 3f(x² – 4x) = m có ít nhất ba nghiệm thực phân biệt thuộc khoảng (0; +∞)?

Phân tích đa thức thành nhân tử (x + y)³ – ( x – y)³.

Phân tích đa thức sau thành nhân tử: x² + 6x + 9.

Cho \(A = \frac{1}{{2 + 2\sqrt a }} + \frac{1}{{2 - 2\sqrt a }} - \frac{{{a^2} + 1}}{{1 - {a^2}}}\)

a) Tìm điều kiện xác định rồi rút gọn A

b) Tìm a để \[{\rm{A}} < \frac{1}{3}\].

Trong mặt phẳng tọa độ Oxy, phương trình đường tròn (C') là ảnh của đường tròn qua (C): x² + y² – 2x + 4y – 1 = 0 với \(\overrightarrow v = \left( {1;2} \right)\) là:

Cho hàm số \((C):y = \frac{{x + 2}}{{x - 1}}\)

Cho điểm M(0; m). Xác định m để từ A kẻ được 2 tiếp tuyến đến (C) sao cho 2 tiếp tuyến tương ứng nằm về hai phía đối với trục Ox.

Tìm các số nguyên x, y thỏa mãn x³ + 2x² + 3x + 2 = y³.

Cho các số dương x, y, z thỏa mãn điều kiện xy + yz + zx = xyz. Chứng minh rằng:

\(\sqrt {x + yz} + \sqrt {y + x{\rm{z}}} + \sqrt {z + xy} \ge \sqrt {xyz} + \sqrt x + \sqrt y + \sqrt z \).

Tìm tất cả các giá trị của tham số m để hàm số y = x³ + x² + mx + 1 đồng biến trên khoảng (–∞; +∞)

Cho hàm số y = – x³ + 3x² + 3mx – 1, tìm tất cả các giá trị của tham số m để hàm số nghịch biến trên khoảng (0; +∞)

Tính tổng: S = 1² + 2² + 3² + ... + n².

Cho tam giác ABC có cạnh a, b, c thỏa mãn bc = a².

Chứng minh rằng sinB.sinC = sin²A và h_b . h_c = h_a².

Cho tam giác ABC có cạnh a, b, c thỏa mãn bc = a².

Chứng minh rằng sinB.sinC = sin²A và h_b . h_c = h_a².

Thực hiện phép tính: (10² + 11² + 12²) : (13² + 14²).

Khai triển (x – 2)².

Cho a, b, c là 3 cạnh trong tam giác. Chứng minh rằng:

\(\frac{a}{{b + c - a}} + \frac{b}{{a + c - b}} + \frac{c}{{a + b - c}} \ge 3\).

Cho tam giác ABC vuông tại A, đường cao AH. Chứng minh:

a) AB² = BH . BC

b) AC² = CH . BC

c) \(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}\).

Với a, b, c là các số dương, chứng minh rằng

\(\left( {a + b + c} \right)\left( {\frac{1}{a} + \frac{1}{b} + \frac{1}{c}} \right) \ge 9\).

Tìm giá trị nhỏ nhất của x² + 3x + 4.

Cho hàm số f(x) có bảng xét dấu của đạo hàm như sau:

Hàm số y = 3f(x + 2) – x³ + 3x đồng biến trên khoảng nào dưới đây?

Tổng các nghiệm của phương trình 3^x+1 + 3^1-x = 10.

Rút gọn các phân thức sau:

a) \(\frac{{{y^3} - {x^3}}}{{{x^3} - 3{{\rm{x}}^2}y + 3{\rm{x}}{y^2} - {y^3}}}\)

b) \(\frac{{{x^5} + x + 1}}{{{x^3} + {x^2} + x}}\)

c) \(\frac{{2{{\rm{x}}^2} - x - 3}}{{{x^2} - 4x - 5}}\).

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của SA, SB.

a) Tìm giao tuyến của (SAC) và (SBD)

b) Tìm giao điểm DN với (SAC)

c) Chứng minh MN // (SCD).

Phân tích đa thức sau thành nhân tử bằng phương pháp nhóm hạng tử:

x² – 2x – 4y² – 4y.

Phân tích đa thức thành nhân tử: x³ – 7x – 6.

Cho A = 5ⁿ⁺² + 26 . 5ⁿ + 8^{2n + 1}. Chứng minh A ⋮ 59.

Chứng minh rằng a⁴ + b⁴ + c⁴ ≥ abc(a + b + c).