7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án (Phần 33)

Lời giải

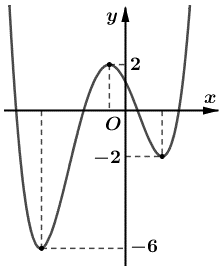
Xét phương trình f(x) = 0 ⇔ mx + m – 1 = 0.

Trường hợp 1: m = 0.

Khi đó phương trình f(x) = 0 ⇔ 0.x = 1 (vô nghiệm).

Vì vậy ta loại m = 0.

Trường hợp 2: m ≠ 0.

Phương trình \(f\left( x \right) = 0 \Leftrightarrow x = \frac{{1 - m}}{m}\).

Phương trình f(x) = 0 có nghiệm thuộc (3; 4).

\( \Leftrightarrow \left\{ \begin{array}{l}\frac{{1 - m}}{m} > 3\\\frac{{1 - m}}{m} < 4\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}\frac{{1 - 4m}}{m} > 0\\\frac{{1 - 5m}}{m} < 0\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}0 < m < \frac{1}{4}\\\left[ \begin{array}{l}m < 0\\m > \frac{1}{5}\end{array} \right.\end{array} \right.\)\( \Leftrightarrow \frac{1}{5} < m < \frac{1}{4}\).

So với điều kiện m ≠ 0, ta nhận \(\frac{1}{5} < m < \frac{1}{4}\).

Vậy \(\frac{1}{5} < m < \frac{1}{4}\) thỏa mãn yêu cầu bài toán.

Lời giải

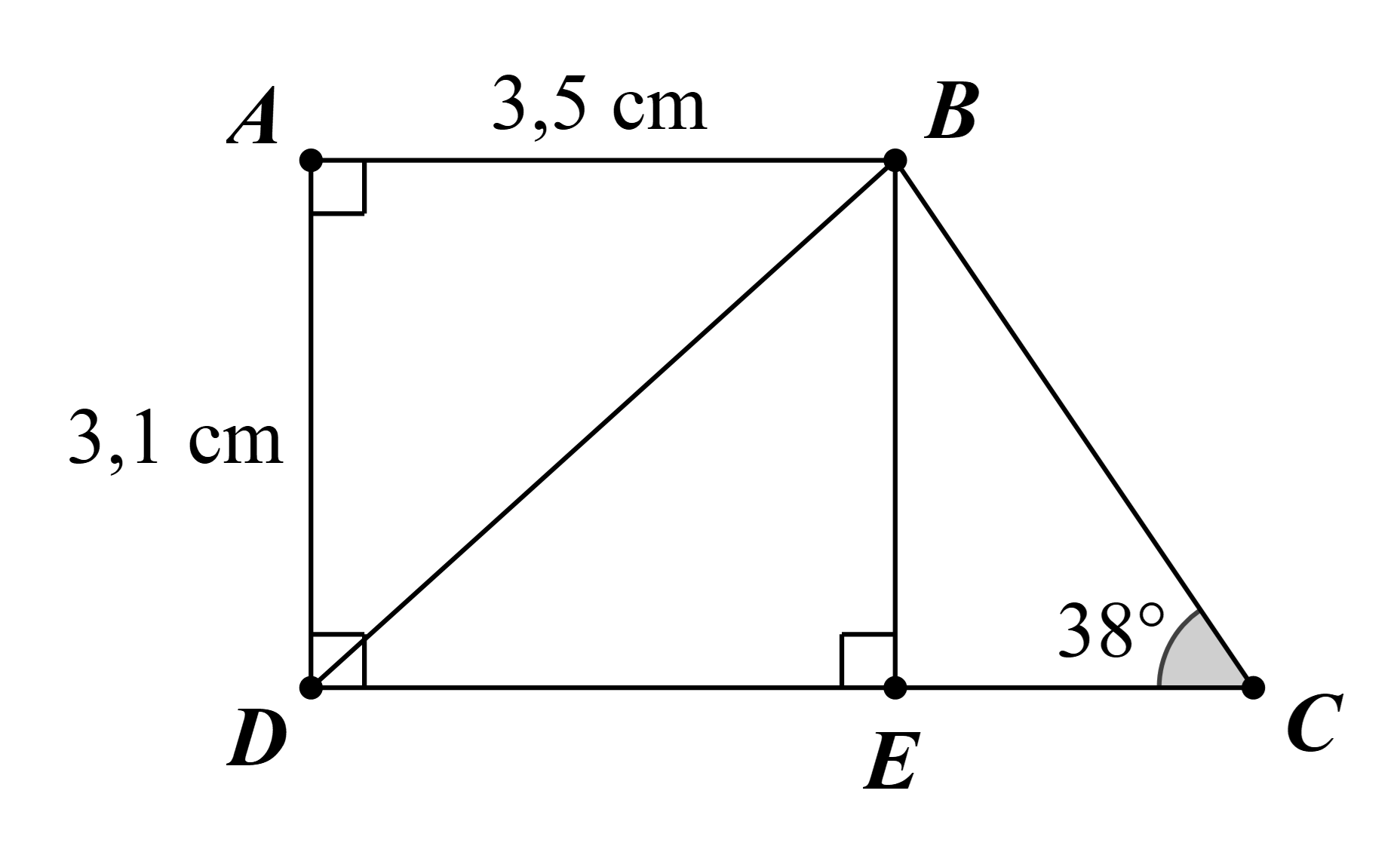
Kẻ BE ⊥ CD tại E.

Ta có AB // CD và AD ⊥ DC.

Suy ra AB ⊥ AD.

Khi đó tứ giác ABED là hình chữ nhật.

Vì vậy DE = AB = 3,5 cm và BE = AD = 3,1 cm.

Tam giác BEC vuông tại E: \(EC = \frac{{BE}}{{\tan \widehat {BCE}}} = \frac{{3,1}}{{\tan 38^\circ }} \approx 3,97\) (cm).

Khi đó DC = DE + EC ≈ 3,5 + 3,97 ≈ 7,47 (cm).

Diện tích hình thang ABCD là:

\(S = \frac{{AD.\left( {AB + DC} \right)}}{2} \approx \frac{{3,1.\left( {3,5 + 7,47} \right)}}{2} \approx 17,0035\) (cm²).

Vậy diện tích hình thang ABCD bằng 17,0035 cm².

Lời giải

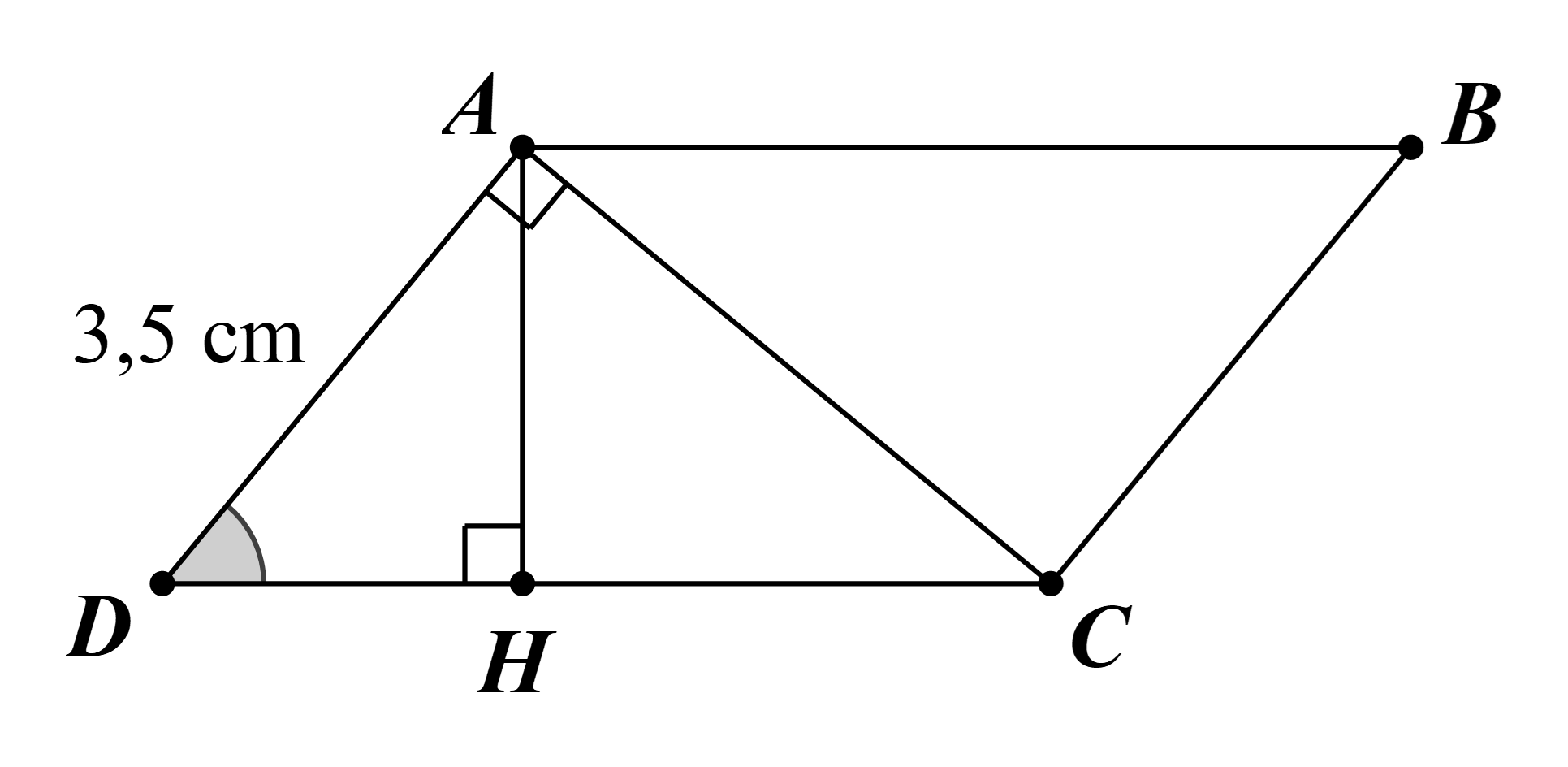
Tam giác ACD vuông tại A: \(CD = \frac{{AD}}{{\cos \widehat {ADC}}} = \frac{{3,5}}{{\cos 60^\circ }} = 7\) (cm).

Kẻ AH ⊥ CD tại H.

Tam giác ADH vuông tại H: \[AH = AD.\sin \widehat {ADH} = 3,5.\sin 60^\circ = \frac{{7\sqrt 3 }}{4}\] (cm).

Diện tích hình bình hành ABCD là: \(S = AH.CD = \frac{{7\sqrt 3 }}{4}.7 = \frac{{49\sqrt 3 }}{4}\) (cm²).

Vậy diện tích hình bình hành ABCD bằng \(\frac{{49\sqrt 3 }}{4}\) cm².

Lời giải

Do hạ giá 10% nên giá bán mới bằng 90% giá bình thường.

Coi giá vốn là 100% thì giá bán mới bằng 108% giá vốn.

Như vậy \(\frac{{108}}{{100}}\) (giá vốn) = \(\frac{{90}}{{100}}\) (giá bình thường).

Giá bình thường so với giá vốn là:

\(\frac{{108}}{{100}}:\frac{{90}}{{100}} = \frac{6}{5} = 120\% \).

Nếu không giảm giá thị cửa hàng lãi là:

120% – 100% = 20%.

Đáp số: 20%.

Lời giải

Ta có \(\frac{1}{{{a^2} + {b^2}}} + \frac{1}{{2ab}} - \frac{1}{{2ab}}\)

Áp dụng bất đẳng thức Cauchy, ta được:

\(\frac{1}{{{a^2} + {b^2}}} + \frac{1}{{2ab}} \ge \frac{4}{{{a^2} + {b^2} + 2ab}} = \frac{4}{{{{\left( {a + b} \right)}^2}}} = \frac{4}{{{1^2}}} = 4\)        (1)

Áp dụng bất đẳng thức Cauchy, ta được: 4ab ≤ (a + b)² = 1² = 1.

\( \Rightarrow \frac{2}{{4ab}} \ge \frac{2}{1}\) \( \Rightarrow \frac{1}{{2ab}} \ge 2\)       (2)

Lấy (1) trừ (2) vế theo vế, ta được: \(\frac{1}{{{a^2} + {b^2}}} + \frac{1}{{2ab}} - \frac{1}{{2ab}} \ge 4 - 2\).

Vậy \(\frac{1}{{{a^2} + {b^2}}} \ge 2\) (điều phải chứng minh).

Dấu “=” xảy ra \( \Leftrightarrow a = b = \frac{1}{2}\).

Lời giải

Ta có BB’ // (ACC’A’) và AC’ ⊂ (ACC’A’).

Suy ra d(BB’, AC’) = d(BB’, (ACC’A’)) = d(B, (ACC’A’)).

Gọi J là trung điểm AC.

Khi đó IJ là đường trung bình của tam giác ABC.

Suy ra IJ // AB và \(IJ = \frac{{AB}}{2} = \frac{a}{2}\).

Mà AB ⊥ AC.

Do đó IJ ⊥ AC.

Mà A’I ⊥ AC (do A’I ⊥ (ABC)).

Suy ra AC ⊥ (A’IJ).

Trong (A’IJ): kẻ IK ⊥ A’J tại K.

Khi đó AC ⊥ IK.

Mà IK ⊥ A’J.

Do đó IK ⊥ (ACC’A’).

Vì vậy d(I, (ACC’A’) = IK.

Tam giác ABC vuông tại A có AI là đường trung tuyến.

Suy ra \(AI = IB = IC = \frac{{BC}}{2} = \frac{{\sqrt {A{B^2} + A{C^2}} }}{2} = a\).

Tam giác AA’I vuông tại I: \(A'I = \sqrt {A{{A'}^2} - A{I^2}} = a\sqrt 3 \).

Tam giác A’IJ vuông tại I có IK là đường cao: \[\frac{1}{{I{K^2}}} = \frac{1}{{A'{I^2}}} + \frac{1}{{I{J^2}}} = \frac{{13}}{{3{a^2}}}\].

Suy ra \(IK = \frac{{a\sqrt {39} }}{{13}}\).

Do đó \(d\left( {B,\left( {ACC'A'} \right)} \right) = \frac{{CB}}{{CI}}.d\left( {I,\left( {ACC'A'} \right)} \right) = 2.IK = \frac{{2a\sqrt {39} }}{{13}}\).

Vậy khoảng cách giữa BB’ và AC’ bằng \(\frac{{2a\sqrt {39} }}{{13}}\).

Lời giải

Ta có \(\overrightarrow {AB} .\overrightarrow {CB} = AB.CB.\cos \widehat B = AB.CB.\frac{{AB}}{{BC}} = A{B^2} = 4\).

Suy ra AB = 2.

Lại có \(\overrightarrow {AC} .\overrightarrow {BC} = AC.BC.\cos \widehat C = AC.BC.\frac{{AC}}{{BC}} = A{C^2} = 9\).

Suy ra AC = 3.

Ta có \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{2^2} + {3^2}} = \sqrt {13} \).

Vậy AB = 2; AC = 3; \(BC = \sqrt {13} \).