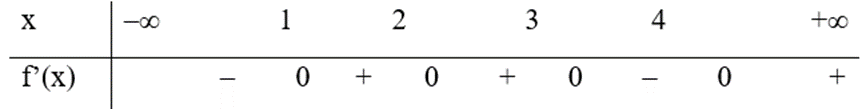Quảng cáo
Trả lời:
Ta có:
n2 – n = n(n – 1)
⇔ n2 = (n – 1)n + n
Khi đó:
S = 12 + 22 + 32 + ... + n2
S = 1 + 1 . 2 + 2 . 3 + ... + (n – 1)n + n
S = [1 . 2 + 2 . 3 + ... + (n – 1)n] + (1 + 2 + ... + n)
\[{\rm{S}} = \frac{{\left( {n - 1} \right)n\left( {n + 1} \right)}}{3} + \frac{{n\left( {n + 1} \right)}}{2}\]
\[{\rm{S}} = \frac{{2\left( {n - 1} \right)n\left( {n + 1} \right) + 3n\left( {n + 1} \right)}}{6}\]
\[{\rm{S}} = \frac{{n\left( {n + 1} \right)\left( {2n - 2 + 3} \right)}}{6}\]
\[{\rm{S}} = \frac{{n\left( {n + 1} \right)\left( {2n + 1} \right)}}{6}\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. P = 3
B. P = 1
C. P = 9
D. \(P = \frac{1}{3}\).
Lời giải
Đáp án đúng là: C
Ta có:
\(P = {\log _{\sqrt[3]{a}}}{a^3} = {\log _{{a^{\frac{1}{3}}}}}{a^3} = 3.3{\log _a}a = 9\,\,\left( {a > 0,a \ne 1} \right)\)
Vậy ta chọn đáp án C.
Câu 2
A. (1; +∞)
B. (–∞; –1)
C. (–1; 0)
D. (0; 2).
Lời giải
Đáp án đúng là: C
Ta có: y’ > 0 ⇔ 3f’(x + 2) – 3x2 + 3 > 0
⇔ 3f’(x + 2) > 3x2 – 3
⇔ f’(x + 2) > x2 – 1
Đặt t = x + 2, suy ra x = t – 2.
Khi đó f’(t) > (t – 2)2 – 1
Chọn t sao cho \(\left\{ \begin{array}{l}{\left( {t - 2} \right)^2} - 1 < 0\\f'\left( t \right) > 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l} - 1 < t - 2 < 1\\t \in \left( {1;2} \right) \cup \left( {2;3} \right) \cup \left( {4; + \infty } \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1 < t < 3\\t \in \left( {1;2} \right) \cup \left( {2;3} \right) \cup \left( {4; + \infty } \right)\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}1 < t < 2\\2 < t < 3\end{array} \right. \Rightarrow \left[ \begin{array}{l}1 < x + 2 < 2\\2 < x + 2 < 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l} - 1 < x < 0\\0 < x < 1\end{array} \right.\)
Suy ra hàm số đã cho đồng biến trên khoảng (–1; 0) và (0; 1).
Vậy ta chọn đáp án C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.