Cho hình vuông ABCD có AB = 12 cm. Trên cạnh CD lấy điểm E sao cho DE = 5 cm. Tia phân giác của góc BAE cắt BC tại F. Trên tia đối của tia BC lấy điểm M sao cho BM = DE.
Chứng minh AE = AM = FM.
Cho hình vuông ABCD có AB = 12 cm. Trên cạnh CD lấy điểm E sao cho DE = 5 cm. Tia phân giác của góc BAE cắt BC tại F. Trên tia đối của tia BC lấy điểm M sao cho BM = DE.
Chứng minh AE = AM = FM.
Câu hỏi trong đề: Giải SBT Toán 8 Cánh Diều Hình vuông có đáp án !!
Quảng cáo
Trả lời:
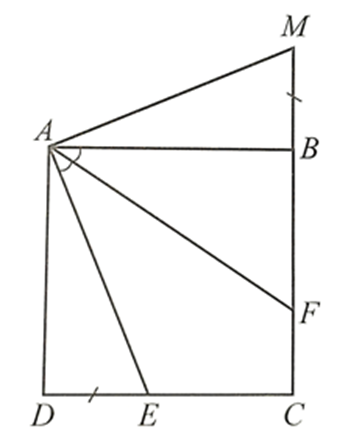
Do ABCD là hình vuông nên AB = AD, \(\widehat {ADC} = \widehat {ABC} = 90^\circ \)
Ta có: \(\widehat {ABM} + \widehat {ABC} = 180^\circ \) (2 góc kề bù) nên \(\widehat {ABM} = 180^\circ - \widehat {ABC} = 180^\circ - 90^\circ = 90^\circ \)
Xét ∆ADE và ∆ABM có:
\(\widehat {ADE} = \widehat {ABM} = 90^\circ \), AD = AB, DE = BM
Do đó ∆ADE = ∆ABM (hai cạnh góc vuông)
Suy ra AE = AM (1) và \(\widehat {DAE} = \widehat {BAM}\).
Do AF là tia phân giác của \(\widehat {BAE}\) nên \(\widehat {EAF} = \widehat {BAF}\).
Suy ra \(\widehat {DAE} + \widehat {EAF} = \widehat {BAM} + \widehat {BAF}\) hay \(\widehat {DAF} = \widehat {MAF}\).
Mà \(\widehat {DAF} = \widehat {MFA}\) (hai góc so le trong do AD // BC), suy ra \(\widehat {MFA} = \widehat {MAF}\).
Do đó, tam giác MAF cân tại M nên AM = FM (2)
Từ (1) và (2) suy ra AE = AM = FM.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
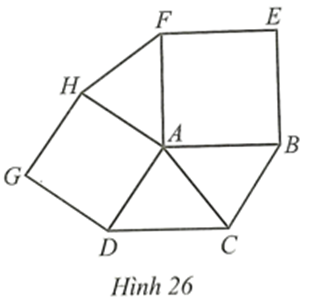
Ta có: \(\widehat {HAK} + \widehat {DAH} + \widehat {DAC} = \widehat {CAK} = 180^\circ \) và \(\widehat {DAH} = 90^\circ \) nên \(\widehat {HAK} + \widehat {DAC} = 90^\circ \).
Mà \(\widehat {AHF} = \widehat {DAC}\) (vì DHAF = DADC chứng minh câu a), suy ra \(\widehat {HAK} + \widehat {AHF} = 90^\circ \).
Trong tam giác AHK, ta có: \(\widehat {AKH} + \widehat {HAK} + \widehat {AHF} = 180^\circ \).
Suy ra \(\widehat {AKH} = 180^\circ - \left( {\widehat {HAK} + \widehat {AHF}} \right) = 180^\circ - 90^\circ = 90^\circ \).
Vậy AK ⊥ HK hay AC ⊥ HF.
Lời giải
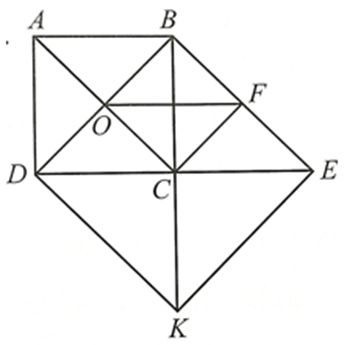
• Tứ giác ABCD là hình vuông suy ra \(\widehat {ACB} = 45^\circ ,OB = OC,\widehat {BOC} = \widehat {DOC} = 90^\circ \).
Do BE // AC suy ra \(\widehat {OBF} = \widehat {DOC}\) (hai góc đồng vị) và \(\widehat {CBE} = \widehat {ACB} = 45^\circ \) (hai góc so le trong).
Xét ∆DBC vuông tại C có: \(\widehat {CDB} + \widehat {CBD} = 90^\circ \)
Suy ra \(\widehat {CDB} = 90^\circ - \widehat {CBD} = 90^\circ - 45^\circ = 45^\circ \)
Xét ∆BCE vuông tại C có: \(\widehat {CBE} + \widehat {CEB} = 90^\circ \)
Suy ra \(\widehat {CBE} = 90^\circ - \widehat {CBE} = 90^\circ - 45^\circ = 45^\circ \)
Do đó \(\widehat {CDB} = \widehat {BEC} = 45^\circ \)
Tam giác BDE có: \(\widehat {DBE} = \widehat {DBC} + \widehat {CBE} = 45^\circ + 45^\circ = 90^\circ \) và \(\widehat {CDB} = \widehat {BEC} = 45^\circ \)
Suy ra tam giác BDE vuông cân tại B nên BD = BE
Tam giác BCE vuông tại C có \(\widehat {CBE} = \widehat {CEB} = 45^\circ \), suy ra nên là tam giác vuông cân tại C. Do đó BC = EC
Xét ∆BCF và ∆ECF có:
BC = EC, BF = EF (do F là trung điểm của BE), cạnh CF chung
Do đó ∆BCF = ∆ECF (c.c.c). Suy ra \(\widehat {BFC} = \widehat {EFC} = 90^\circ \).
Tứ giác BOCF có \(\widehat {BOC} = \widehat {OBF} = \widehat {BFC} = 90^\circ \) nên BOCF là hình chữ nhật.
Hình chữ nhật BOCF có OB = OC nên BOCF là hình vuông.
• Ta có: BC = CD và BC = CE nên CD = CE.
Tứ giác BDKE có hai đường chéo BK và DE cắt nhau tại trung điểm C của mỗi đường nên BDKE là hình bình hành.
Hình bình hành BDKE có \(\widehat {DBE} = 90^\circ \) nên BDKE là hình chữ nhật.
Hình chữ nhật BDKE có BD = BE nên BDKE là hình vuông.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.