Giải SBT Toán 8 Cánh Diều Hình vuông có đáp án
44 người thi tuần này 4.6 679 lượt thi 13 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 10
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 09
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 08
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 07
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 06
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 05
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 04
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 03
Danh sách câu hỏi:
Lời giải
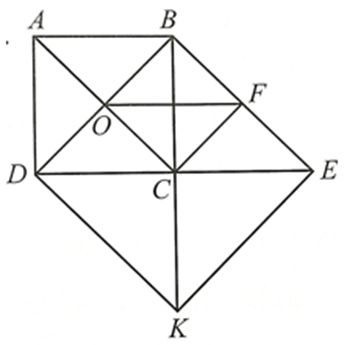
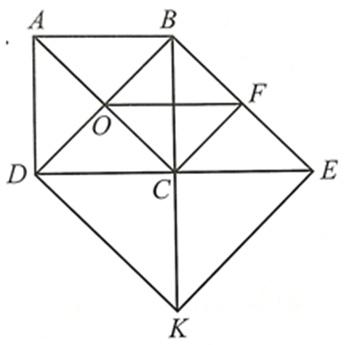
• Tứ giác ABCD là hình vuông suy ra \(\widehat {ACB} = 45^\circ ,OB = OC,\widehat {BOC} = \widehat {DOC} = 90^\circ \).
Do BE // AC suy ra \(\widehat {OBF} = \widehat {DOC}\) (hai góc đồng vị) và \(\widehat {CBE} = \widehat {ACB} = 45^\circ \) (hai góc so le trong).
Xét ∆DBC vuông tại C có: \(\widehat {CDB} + \widehat {CBD} = 90^\circ \)
Suy ra \(\widehat {CDB} = 90^\circ - \widehat {CBD} = 90^\circ - 45^\circ = 45^\circ \)
Xét ∆BCE vuông tại C có: \(\widehat {CBE} + \widehat {CEB} = 90^\circ \)
Suy ra \(\widehat {CBE} = 90^\circ - \widehat {CBE} = 90^\circ - 45^\circ = 45^\circ \)
Do đó \(\widehat {CDB} = \widehat {BEC} = 45^\circ \)
Tam giác BDE có: \(\widehat {DBE} = \widehat {DBC} + \widehat {CBE} = 45^\circ + 45^\circ = 90^\circ \) và \(\widehat {CDB} = \widehat {BEC} = 45^\circ \)
Suy ra tam giác BDE vuông cân tại B nên BD = BE
Tam giác BCE vuông tại C có \(\widehat {CBE} = \widehat {CEB} = 45^\circ \), suy ra nên là tam giác vuông cân tại C. Do đó BC = EC
Xét ∆BCF và ∆ECF có:
BC = EC, BF = EF (do F là trung điểm của BE), cạnh CF chung
Do đó ∆BCF = ∆ECF (c.c.c). Suy ra \(\widehat {BFC} = \widehat {EFC} = 90^\circ \).
Tứ giác BOCF có \(\widehat {BOC} = \widehat {OBF} = \widehat {BFC} = 90^\circ \) nên BOCF là hình chữ nhật.
Hình chữ nhật BOCF có OB = OC nên BOCF là hình vuông.
• Ta có: BC = CD và BC = CE nên CD = CE.
Tứ giác BDKE có hai đường chéo BK và DE cắt nhau tại trung điểm C của mỗi đường nên BDKE là hình bình hành.
Hình bình hành BDKE có \(\widehat {DBE} = 90^\circ \) nên BDKE là hình chữ nhật.
Hình chữ nhật BDKE có BD = BE nên BDKE là hình vuông.
Lời giải
Tứ giác CDOF có \(\widehat {ODC} = 45^\circ \) nên không thể là hình vuông.
Lời giải
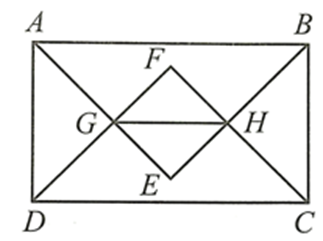
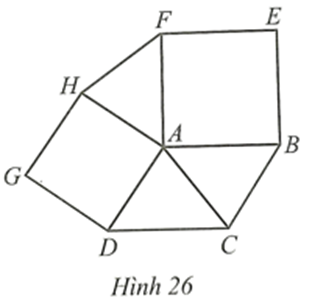
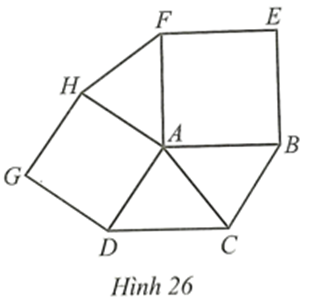
Do ABCD là hình chữ nhật nên \(\widehat {DAB} = \widehat {ABC} = \widehat {BCD} = \widehat {CDA} = 90^\circ \)
Mà AE, BE, CF, DF lần lượt là các tia phân giác của các \(\widehat {BAD},\widehat {ABC},\widehat {BCD},\widehat {ADC}\)
Suy ra \(\widehat {DAE} = \widehat {EAB} = \widehat {ABE} = \widehat {EBC} = \widehat {BCF} = \widehat {FCD} = \widehat {CDF} = \widehat {FDA} = \frac{{90^\circ }}{2} = 45^\circ {\rm{.\;}}\)
Xét ∆ADG có: \(\widehat {ADG} + \widehat {AGD} + \widehat {GAD} = 180^\circ \)
Suy ra \(\widehat {AGD} = 180^\circ - \left( {\widehat {ADG} + \widehat {GAD}} \right) = 180^\circ - \left( {45^\circ + 45^\circ } \right) = 90^\circ \)
Do đó ∆ADG vuông cân tại G
Chứng minh tương tự các tam giác EAB, FCD, HBC đều là tam giác vuông cân.
Xét ∆GAD và ∆HBC có:
\(\widehat {GAD} = \widehat {GDA} = \widehat {HBC} = \widehat {HCB} = 45^\circ \), cạnh AD = BC (do ABCD là hình chữ nhật)
Do đó ∆GAD = ∆HBC (g.c.g).
Suy ra GD = HC (hai cạnh tương ứng).
Mà FD = FC, suy ra FG = FH.
∆GFH có: \(\widehat {GFH} = 90^\circ \) và FG = FH
Do đó, tam giác FGH vuông cân tại F. Suy ra \(\widehat {FGH} = 45^\circ \).
Ta có: \(\widehat {FGH} = \widehat {CDF} = 45^\circ \) và \(\widehat {FGH},\widehat {CDF}\) nằm ở vị trí đồng vị nên GH // CD.
Lời giải
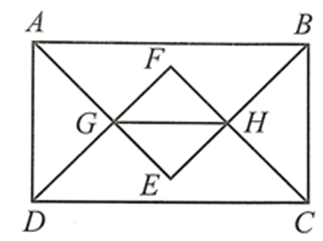
Ta có \(\widehat {EGF} = \widehat {AGD} = 90^\circ \) (hai góc đối đỉnh).
Tứ giác GFHE có \(\widehat {EGF} = \widehat {GFH} = \widehat {HEG} = 90^\circ \) nên GFHE là hình chữ nhật.
Hình chữ nhật GFHE có FG = FH nên GFHE là hình vuông.
Lời giải
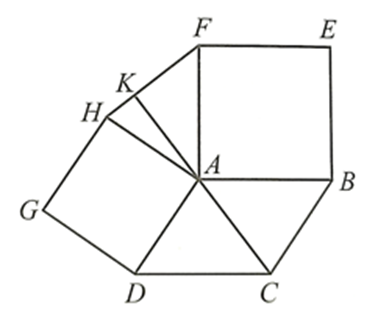
Gọi K là giao điểm của AC và HF.
Do ABEF và ADGH đều là hình vuông nên \(\widehat {BAF} = \widehat {DAH} = 90^\circ \), AF = AB, AH = AD.
Do ABCD là hình bình hành nên AB = DC
Mà AF = AB nên AF = DC.
Ta có: \(\widehat {HAF} + \widehat {FAB} + \widehat {DAB} + \widehat {DAH} = 360^\circ \)
Mà \(\widehat {BAF} = \widehat {DAH} = 90^\circ \) nên \(\widehat {HAF} + \widehat {DAB} = 360^\circ - \left( {90^\circ + 90^\circ } \right) = 180^\circ \) (1)
Hình bình hành ABCD có AB // DC nên \(\widehat {ADC} + \widehat {DAB} = 180^\circ \) (2)
Từ (1) và (2) suy ra \(\widehat {HAF} = \widehat {ADC}\).
Xét ∆HAF và ∆ADC có:
AH = AD, \(\widehat {HAF} = \widehat {ADC}\), AF = DC
Suy ra DHAF = DADC (c.g.c).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.