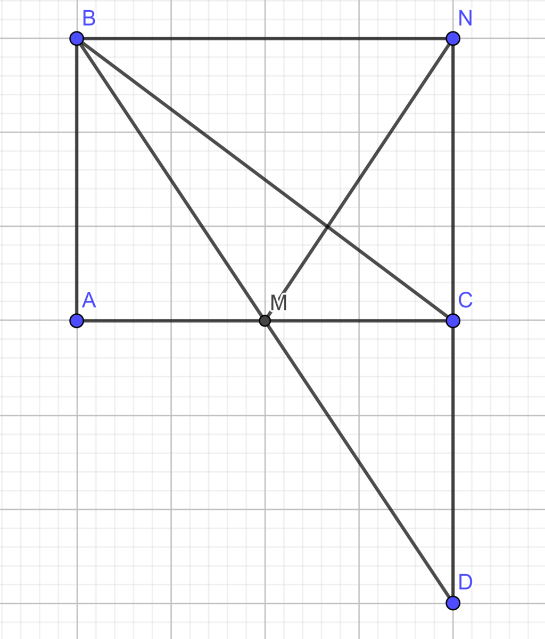
cho tam giác ABC vuông tại A. Gọi M là trung điểm của AC , trên tia đối của tia MB lấy điểm D sao cho MD = MB.
1) Chứng minh AD = BC.
2) Chứng minh CD vuông góc với AC.
3) Đường thẳng qua B song song với AC cắt tia DC tại N. Chứng minh ∆ABM = ∆CNM.
cho tam giác ABC vuông tại A. Gọi M là trung điểm của AC , trên tia đối của tia MB lấy điểm D sao cho MD = MB.
1) Chứng minh AD = BC.
2) Chứng minh CD vuông góc với AC.
3) Đường thẳng qua B song song với AC cắt tia DC tại N. Chứng minh ∆ABM = ∆CNM.
Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
1) Xét ΔCBM và ΔADM có:
AM = MC (giả thtết)
( đối đỉnh)
BM = MD (giả thiết)
⇒ ΔCBM = ΔADM (c.g.c)
Suy ra: BC = DA (hai cạnh tương ứng)
2) Xét ΔABM và ΔCDM có:
AM = CM (giả thiết)
(đối đỉnh)
BM = DM (giả thiết)
⇒ ΔABM = ΔCDM (c.g.c)
= 90°(hai góc tương ứng) (đpcm)
⇒ DC⊥AC (đpcm)
3) Ta có BN // AC mà AC ⊥ DC ⇒ BN ⊥ DC ⇒ = 90°
AB // CD (do cùng ⊥AC)
Xét ΔABC và ΔNBC có:
(hai góc ở vị trí so le trong)
BC chung
(do BN//AC nên đó là hai góc ở vị trí so le trong)
⇒ ΔABC = ΔNBC (g.c.g)
⇒ AB = NC (hai cạnh tương ứng)
Xét ΔABM và ΔCNM có:
AB = CN (cmt)
= 90°
AM = CM (giả thiết)
⇒ ΔABM = ΔCNM (đpcm).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
1 cm3 = 10-3 dm3 = 10-6 m3 = 0,000001 m3
Như vậy để đổi cm3 sang m3 trên máy tính ta lấy đơn vị cm3 nhân với 10-6 hoặc chia cho 1000000.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi thời gian tổ I hoàn thành công việc riêng là x (x > 0, giờ),
thời gian tổ II hoàn thành công việc riêng là y (y > 0, giờ)
Trong 1 giờ, tổ I làm được (công việc)
Trong 1 giờ, tổ II làm được (công việc)
Trong 1 giờ, cả 2 tổ làm được (công việc)
Nên ta có phương trình: (1)
Trong 10 giờ, tổ I làm được (công việc)
Vì sau 2 giờ làm chung thì tổ II được điều đi làm việc khác, tổ I hoàn thành công việc còn lại trong 10 giờ nên ta có phương trình:
⇔ 2. + = 1
⇔ x = 15
Thay vào (1) tìm được y = 10
Vậy thời gian tổ I hoàn thành công việc riêng là 15 giờ.
thời gian tổ II hoàn thành công việc một mình là 10 giờ.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập
Mai
còn mấy câu nx cơ,ko pk riêng câu này đ
Mai
có cần gửi link hay hình ảnh ko
Mai
lấy câu trl vs ảnh vẽ bên HĐ mà tự nhận bên mik giải
Xem tất cả 1 phản hồi
Quyên Đỗ (Capybaraa)
HĐ là j ??