Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 140kg chất A và 9kg chất B. Từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng, có thể chiết xuất được 20kg chất A và 0,6kg chất B. Từ mỗi tấn nguyên liệu loại II giá triệu đồng có thể chiết xuất được 10kg chất A và 1,5kg chất B. Hỏi phải dùng bao nhiêu tấn nguyên liệu mỗi loại để chi phí mua nguyên liệu là ít nhất, biết rằng cơ sở cung cấp nguyên liệu chỉ có cung cấp không quá 10 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại
Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi x là số tấn nguyên liệu loại I, y là số tấn nguyên liệu loại II cần dùng.
Số tiền để mua nguyên liệu là 4x + 3y (triệu đồng)
Theo bài ra ta có hệ bất phương trình: (1)
Yêu cầu bài toán trở thành: Tìm (x; y) thỏa mãn (1) để F(x; y) = 4x + 3y đạt giá trị nhỏ nhất
Vẽ và xác định miền nghiệm của (1)
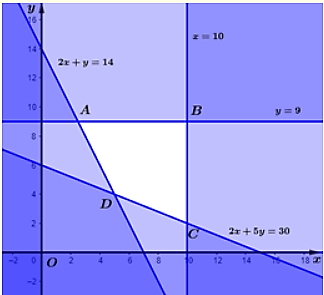
Miền nghiệm của (1) là tứ giác ABCD (kể cả biên)
F(x; y) = 4x + 3y
F(A) = 37; F(B) = 67; F(C) = 32; F(D) = 32
Suy ra: min F(x; y) = F(D) = 32 khi x = 5; y = 4
Vậy để chi phí mua nguyên liệu là ít nhất thì cần mua 5 tấn nguyên liệu loại I và 4 tấn nguyên liệu loại II.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
1 cm3 = 10-3 dm3 = 10-6 m3 = 0,000001 m3
Như vậy để đổi cm3 sang m3 trên máy tính ta lấy đơn vị cm3 nhân với 10-6 hoặc chia cho 1000000.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi thời gian tổ I hoàn thành công việc riêng là x (x > 0, giờ),
thời gian tổ II hoàn thành công việc riêng là y (y > 0, giờ)
Trong 1 giờ, tổ I làm được (công việc)
Trong 1 giờ, tổ II làm được (công việc)
Trong 1 giờ, cả 2 tổ làm được (công việc)
Nên ta có phương trình: (1)
Trong 10 giờ, tổ I làm được (công việc)
Vì sau 2 giờ làm chung thì tổ II được điều đi làm việc khác, tổ I hoàn thành công việc còn lại trong 10 giờ nên ta có phương trình:
⇔ 2. + = 1
⇔ x = 15
Thay vào (1) tìm được y = 10
Vậy thời gian tổ I hoàn thành công việc riêng là 15 giờ.
thời gian tổ II hoàn thành công việc một mình là 10 giờ.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập
Anh Vũ Nguyễn Lê
Tại sao ra 2x+5y=30 vậy ạ
Xem tất cả 1 phản hồi
Vạn Đỗ Văn
Tại vì quy đồng tất cả cho 10/3