Câu hỏi:

13/07/2024 2,425

Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), tam giác ABC vuông tại B. Biết SA = 2a, AB = a, \(BC = a\sqrt 3 \). Tính bán kính R của mặt cầu ngoại tiếp hình chóp đã cho.

Xem lời giải

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

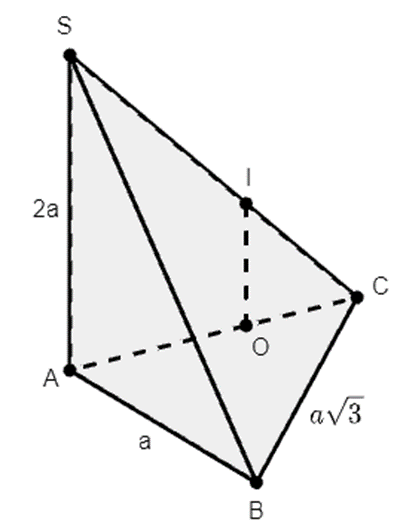
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), tam giác ABC (ảnh 1)

Gọi O, I lần lượt là trung điểm của AC và SC.

Khi đó OI là đường trung bình của tam giác SAC nên OI // SA.

Mà SA⊥(ABC) nên OI ⊥ (ABC).

Tam giác ABC vuông tại B nên O là tâm đường tròn ngoại tiếp tam giác ABC.

Mà OI ⊥ (ABC) nên OI chính là trục của (ABC) suy ra IA = IB = IC (1).

Lại có SA ⊥ (ABC) nên SA ⊥ AC.

Do đó tam giác SAC vuông tại A nên I chính là tâm đường tròn ngoại tiếp tam giác SAC, suy ra IS = IA = IC (2).

Từ (1) và (2) ta có IA = IB = IC = IS, hay I là tâm mặt cầu ngoại tiếp chóp S.ABC và bán kính mặt cầu là \(R = IS = \frac{1}{2}SC\).

Áp dụng định lý Py-ta-go trong tam giác vuông ABC, ta có:

\(AC = \sqrt {A{B^2} + B{C^2}} = 2a\).

Áp dụng định lí Py-ta-go trong tam giác vuông SAC, ta có:

\(SC = \sqrt {S{A^2} + A{C^2}} = 2a\sqrt 2 \)

Vậy \(R = \frac{1}{2}SC = a\sqrt 2 \).

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hàm số f(x) = ax⁴ + bx³ + cx² (a, b, c ∈ ℝ). Hàm số y = f '(x) có đồ thị như trong hình bên. Số nghiệm thực phân biệt của phương trình 2f(x) + 3 = 0.

A. 4;

B. 1;

C. 2;

D. 3.

Lời giải

Đáp án đúng là: C

Từ đồ thị ta có bảng biến thiên:

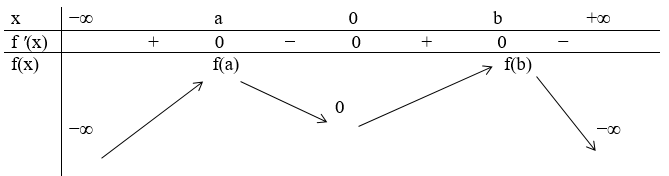
Cho hàm số f(x) = ax^4 + bx^3 + cx^2 (a, b, c thuộc R). Hàm số y = f '(x) có đồ thị như (ảnh 2)

Dựa vào bảng biến thiên thì phương trình 2f(x) + 3 = 0 \( \Leftrightarrow f(x) = - \frac{3}{2}\) có hai nghiệm phân biệt.

Câu 2

Tìm m để đường thẳng y = mx + 1 cắt đồ thị hàm số \(y = \frac{{x + 1}}{{x - 1}}\) tại hai điểm thuộc nhánh của đồ thị.

A. \(m \in \left( {\frac{{ - 1}}{4}; + \infty } \right)\backslash \left\{ 0 \right\}\);

B. m ∈ (0; +∞);

C. m ∈ (−∞; 0);

D. m = 0.

Lời giải

Đáp án đúng là: B

Phương trình hoành độ giao điểm là: \(mx + 1 = \frac{{x + 1}}{{x - 1}}\)

\( \Leftrightarrow \left\{ \begin{array}{l}x \ne 1\\\left( {mx + 1} \right)\left( {x - 1} \right) = x + 1\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}x \ne 1\\f(x) = m{x^2} - mx - 2 = 0\left( 1 \right)\end{array} \right.\)

Theo hệ thức Vi-ét có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 1\\{x_1}{x_2} = \frac{{ - 2}}{m}\end{array} \right.\)

Đường thẳng y = mx + 1 cắt đồ thị hàm số \(y = \frac{{x + 1}}{{x - 1}}\) tại hai điểm thuộc hai nhánh của đồ thị

Khi đó (1) có hai nghiệm phân biệt x₁; x₂ khác 1 thỏa mãn (x₁ – 1)(x₂ – 1) < 0

\( \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\\Delta = {m^2} + 8m > 0\\f(1) \ne 0\\{x_1}{x_2} - \left( {{x_1} + {x_2}} \right) + 1 < 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\\left[ \begin{array}{l}m > 0\\m < - 8\end{array} \right.\\m{.1^2} - m.1 - 2 \ne 0\\ - \frac{2}{m} - 1 + 1 < 0\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m > 0\\m < - 8\end{array} \right.\\\frac{2}{m} > 0\end{array} \right. \Leftrightarrow m > 0\)

Câu 3

Trong không gian với hệ tọa độ Oxyz, mặt phẳng (P) cắt ba trục Ox, Oy, Oz tại A, B, C; trực tâm tam giác ABC là H(1; 2; 3). Phương trình của mặt phẳng (P) là:

A. x + 2y + 3z – 14 = 0;

B. x + 2y + 3z + 14 = 0;

C. \(\frac{x}{1} + \frac{y}{2} + \frac{z}{3} = 1\);

D. \(\frac{x}{1} + \frac{y}{2} + \frac{z}{3} = 0\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Biết AB = BC = a, AD = 2a và SA vuông góc với mặt phẳng (ABCD) và \(SA = a\sqrt 2 \). Gọi M là trung điểm AD. Khoảng cách giữa hai đường thẳng BM và SC bằng

A. \(\frac{a}{2}\);

B. a;

C. \(\frac{{a\sqrt 2 }}{2}\);

D. \(a\sqrt 2 \).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Tìm số các nghiệm nguyên không âm (x; y; z) của phương trình x + y + z = 10.

A. 54;

B. 60;

C. 66;

D. 72.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho hình vuông ABCD có cạnh bằng a và có diện tích S₁. Nối 4 điểm A₁; B₁; C₁; D₁ theo thứ tự của 4 cạnh AB, BC, CD, DA ta được hình vuông thứ hai có diện tích S₂. Tiếp tục làm như thế, ta được hình vuông thứ ba là A₂B₂C₂D₂ có diện tích S₃, … và cứ tiếp tục làm như thế, ta tính được các hình vuông lần lượt có diện tích, … , S₁₀₀ (tham khảo hình bên). Tính tổng S = S₁ + S₂ + S₃ + … + S₁₀₀.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Trong không gian với hệ tọa độ Oxyz , đường thẳng d đi qua điểm A(1; 2; 3) và vuông góc với mặt phẳng (P): 2x + 2y + z + 2017 = 0 có phương trình là

A. \(\frac{{x + 2}}{1} = \frac{{y + 2}}{2} = \frac{{z + 1}}{3}\);

B. \(\frac{{x - 2}}{1} = \frac{{y - 2}}{2} = \frac{{z - 1}}{3}\);

C. \(\frac{{x + 1}}{2} = \frac{{y + 2}}{2} = \frac{{z + 3}}{1}\);

D. \(\frac{{x - 1}}{2} = \frac{{y - 2}}{2} = \frac{{z - 3}}{1}\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), tam giác ABC vuông tại B. Biết SA = 2a, AB = a, \(BC = a\sqrt 3 \). Tính bán kính R của mặt cầu ngoại tiếp hình chóp đã cho.

Bình luận

Cho hàm số f(x) = ax4 + bx3 + cx2 (a, b, c ∈ ℝ). Hàm số y = f '(x) có đồ thị như trong hình bên. Số nghiệm thực phân biệt của phương trình 2f(x) + 3 = 0.

Tìm m để đường thẳng y = mx + 1 cắt đồ thị hàm số \(y = \frac{{x + 1}}{{x - 1}}\) tại hai điểm thuộc nhánh của đồ thị.

Trong không gian với hệ tọa độ Oxyz, mặt phẳng (P) cắt ba trục Ox, Oy, Oz tại A, B, C; trực tâm tam giác ABC là H(1; 2; 3). Phương trình của mặt phẳng (P) là:

Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Biết AB = BC = a, AD = 2a và SA vuông góc với mặt phẳng (ABCD) và \(SA = a\sqrt 2 \). Gọi M là trung điểm AD. Khoảng cách giữa hai đường thẳng BM và SC bằng

Tìm số các nghiệm nguyên không âm (x; y; z) của phương trình x + y + z = 10.

Trong không gian với hệ tọa độ Oxyz , đường thẳng d đi qua điểm A(1; 2; 3) và vuông góc với mặt phẳng (P): 2x + 2y + z + 2017 = 0 có phương trình là

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho hàm số f(x) = ax⁴ + bx³ + cx² (a, b, c ∈ ℝ). Hàm số y = f '(x) có đồ thị như trong hình bên. Số nghiệm thực phân biệt của phương trình 2f(x) + 3 = 0.