Câu hỏi:

15/08/2023 1,227

Cho hình chóp S.ABCD có ABCD là hình thang, đáy lớn BC với BC = 2a, AD = AB = a, mặt bên (SAD) là tam giác đều. Lấy điểm M trên cạnh AB sao cho MB = 2AM. Mặt phẳng (α) đi qua M và song song với SA, BC. Xác định thiết diện của hình chóp bị cắt bởi mặt phẳng (α) và tính diện tích của thiết diện đó.

Xem lời giải

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

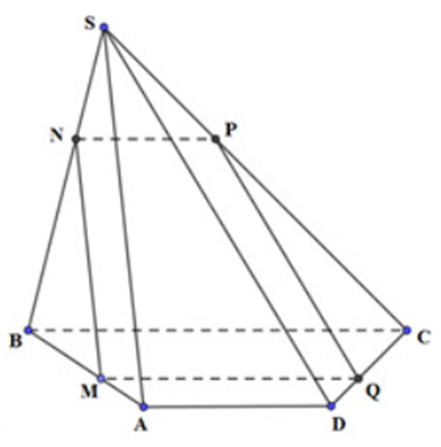
Cho hình chóp S.ABCD có ABCD là hình thang, đáy lớn BC với BC = 2a, AD = AB = a (ảnh 1)

+) Dựng thiết diện:

Qua M kẻ MQ song song BC (Q ∈ DC), kẻ MN song song SA (N ∈ SB)

Qua N kẻ NP song song BC (P ∈ SC)

Khi đó, (MNPQ) là mặt phẳng qua M và song song BC, SA

⇒ (MNPQ) ≡ (α)

Thiết diện của hình chóp bị cắt bởi mặt phẳng (α) là tứ giác MNPQ.

+) Tính diện tích thiết diện:

Ta có: NP // MQ (cùng song song BC) ⇒ MNPQ là hình thang

ΔSAD đều ⇒ SA = SD = AD = a

ABCD là hình thang, MQ // BC ⇒ \(\frac{{CQ}}{{DC}} = \frac{{BM}}{{AB}} = \frac{{BN}}{{SB}} = \frac{2}{3}\)

MN // SA ⇒ \(\frac{{MN}}{{SA}} = \frac{{BM}}{{AB}} = \frac{2}{3}\) ⇒ \(MN = \frac{2}{3}SA = \frac{2}{3}a\)

NP // BC ⇒ \(\frac{{NP}}{{BC}} = \frac{1}{3}\) ⇒ \(NP = \frac{1}{3}BC = \frac{2}{3}a\) và \(\frac{{PC}}{{SC}} = \frac{{NB}}{{SB}} = \frac{2}{3}\) ⇒ \(\frac{{PC}}{{SC}} = \frac{{CQ}}{{DC}} = \frac{2}{3}\)

⇒ \(\frac{{PQ}}{{SD}} = \frac{2}{3}\) ⇒ \(PQ = \frac{2}{3}SD = \frac{2}{3}a.\)

Gọi I, J lần lượt là trung điểm của BM và CQ.

Giả sử MQ có độ dài bằng x. Khi đó, do IJ là đường trung bình của hình thang BCQM

⇒ \(IJ = \frac{{MQ + BC}}{2} = \frac{{x + 2a}}{2}\)

Do MQ là đường trung bình của hình thang IJDA ⇒ 2MQ = IJ + AD

⇔ \(2x = \frac{{x + 2a}}{2} + a\) ⇔ 4x = x + 2a + 2a ⇔ \(x = \frac{4}{3}a\)

⇒ \(MQ = \frac{4}{3}a\)

Xét hình thang MNPQ có: NP = MN = PQ = \(\frac{2}{3}a,\) \(MQ = \frac{4}{3}a\) ⇒ MNPQ là hình thang cân.

Kẻ MH, NK vuông góc với PQ (H, K ∈ PQ)

⇒ \(QH = PK = \frac{{PQ - MN}}{2} = \frac{{\frac{4}{3}a - \frac{2}{3}a}}{2} = \frac{a}{3}\)

⇒ \(MH = \sqrt {M{Q^2} - Q{H^2}} = \sqrt {{{\left( {\frac{2}{3}a} \right)}^2} - {{\left( {\frac{1}{3}a} \right)}^2}} = \sqrt {\frac{{{a^2}}}{3}} = \frac{{a\sqrt 3 }}{3}.\)

Diện tích hình thang MNPQ: \(S = \frac{1}{2}\left( {MN + PQ} \right).MH = \frac{1}{2}.\left( {\frac{2}{3}a + \frac{4}{3}a} \right).\frac{{a\sqrt 3 }}{3} = \frac{{{a^2}\sqrt 3 }}{3}.\)

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Gọi S là tập hợp các số tự nhiên có hai chữ số. Chọn ngẫu nhiên đồng thời hai số từ tập hợp S. tính xác suất để hai số được chọn có chữ số hàng đơn vị giống nhau.

A. \(\frac{8}{{89}}.\)

B. \(\frac{{81}}{{89}}.\)

C. \(\frac{{36}}{{89}}.\)

D. \(\frac{{53}}{{89}}.\)

Lời giải

Đáp án đúng là: A

Số tự nhiên có 2 chữ số là: \(C_9^1.C_{10}^1 = 90\) (số).

\(\Omega :\) “Chọn ngẫu nhiên 2 số từ tập hợp S” ⇒ \({n_\Omega } = C_{90}^2\)

A: “Chọn được 2 số có chữ số hàng đơn vị giống nhau”.

· TH1: Chữ số hàng đơn vị là 0 ⇒ Có 9 chữ số là: 10; 20; 30; 40; 50; 60; 70; 80; 90.

⇒ Số cách chọn 2 số là: \(C_9^2.\)

Tương tự với các số có chữ số hàng đơn vị là: 1; 2; 3; 4; 5; 6; 7; 8; 9.

⇒ Có tất cả 10 trường hợp giống nhau.

⇒ \({n_A} = 10.C_9^2\)

⇒ \({P_A} = \frac{{10.C_9^2}}{{C_{90}^2}} = \frac{8}{{89}}.\)

Câu 2

Trên một kệ sách có 5 quyển sách Toán, 4 quyển sách Lí, 3 quyển sách Văn. Các quyển sách đều khác nhau. Hỏi có bao nhiêu cách sắp xếp các quyển sách trên:

a) Một cách tuỳ ý?

b) Theo từng môn và sách Toán nằm ở giữa?

Xem đáp án

Lời giải

a) Có tất cả 5 + 4 + 3 = 12 quyển sách.

Cách sắp xếp các quyển sách một cách tùy ý là: 12! (cách)

b) Chọn vị trí ở giữa cho 5 quyển sách Toán nên có số cách là 5! (cách)

Chọn vị trí đầu cho sách lý, có số cách là 4! (cách)

Chọn vị trí cuối cho sách văn, có số cách là 3! (cách)

Hoán đổi vị trí đầu và vị trí cuối nên thêm 2! (cách)

Vậy số cách sắp xếp các quyển sách trên theo từng môn và sách Toán nằm ở giữa là:

4!.5!.3!.2! = 34560 (cách)

Câu 3