Phép chiếu xuyên tâm có đặc điểm gì?

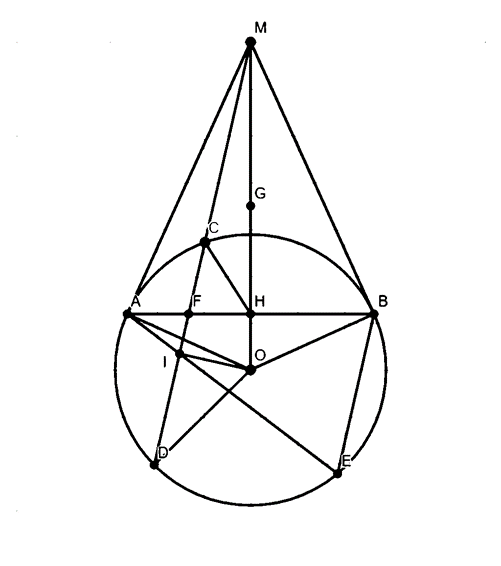
a) Vì MA, MB là tiếp tuyến của (O)

⇒ \(\widehat {MAO} = \widehat {MBO} = 90^\circ \)

Tứ giác AOBM có \(\widehat {MAO} + \widehat {MBO} = 90^\circ + 90^\circ = 180^\circ \)

⇒ A, O, B, M thuộc đường tròn đường kính OM.

⇒ AOBM nội tiếp đường tròn đường kính OM.

Tâm G là trung điểm OM

b. Vì MA là tiếp tuyến của (O)

⇒ \(\widehat {MAC} = \widehat {MDA}\) (góc tạo bởi tiếp tuyến, dây cung và góc nội tiếp cùng chắn cung AC)

Lại có \(\widehat M\)chung.

Do đó, ΔMAC ∽ ΔMDA(g.g)

⇒ \(\frac{{MA}}{{MD}} = \frac{{MC}}{{MA}}\)

⇒ MA² = MC.MD.

c) Vì I là trung điểm CD ⇒ OI ⊥ CD

⇒ OI ⊥ MI

⇒ I thuộc đường tròn đường kính OM

⇒ I ∈ (G)

⇒ M, A, O, I, B ∈ (G).

d) Vì MA, MB là tiếp tuyến của (O)

Nên MA = MB, MO là phân giác \[\widehat {AMB}\]

⇒ ΔMAB có MO vừa là phân giác vừa là đường cao.

⇒ MO ⊥ AB

Áp dụng hệ thức lượng vào ΔAMO đường cao AH có:

⇒ MA² = MH.MO (kết hợp b)

⇒ MH.MO = MC.MD

⇒ \(\frac{{MC}}{{MO}} = \frac{{MH}}{{MD}}\)

Xét ΔMCH và ΔMOD có:

\(\frac{{MC}}{{MO}} = \frac{{MH}}{{MD}}\)

\(\widehat M\)chung

Do đó, ΔMCH ∽ ΔMOD (c.g.c).

⇒ \(\widehat {MHC} = \widehat {MDO} = \widehat {CDO}\)

⇒ CHOD nội tiếp

e) Gọi CD ∩ AB = F

⇒ \(\widehat {AFI} = \widehat {ABE}\) (vì CD // BE và hai góc ở vị trí đồng vị)

Ta có: A, M, B, O, I ∈ (G)

⇒ \(\widehat {AIC} = \widehat {AIM} = \widehat {AOM} = \frac{1}{2}\widehat {AOB} = \widehat {AEB}\)

⇒ \(\widehat {AIF} = \widehat {AEB}\)

⇒ ΔAIF ∽ ΔAEB (g.g).

⇒ \(\widehat {IAF} = \widehat {EAB} = \widehat {EAF}\)

⇒ A, I, E thẳng hàng.

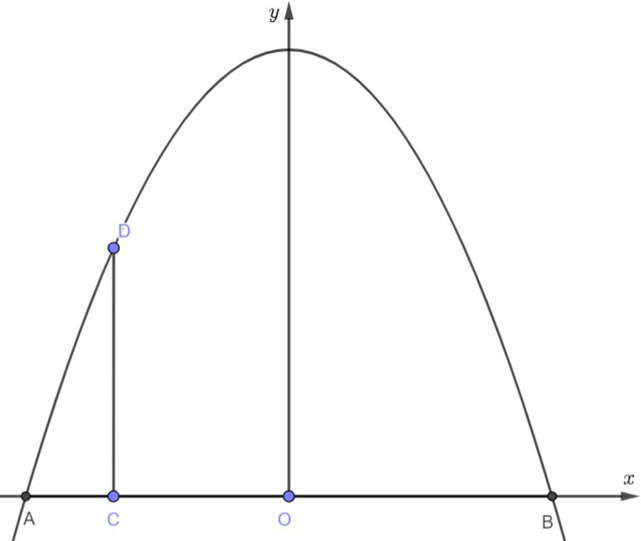
AB = 9m

AC = 0,5m

CD = 1,6m

Gọi O là trung điểm của A

Dựng hệ Oxy thỏa mãn A,B thuộc Ox và Oy ⊥ AB tại O

OB = \(\frac{9}{2}\), OC = \(\frac{9}{2} - 0,5 = 4\)

Cổng là (P) có phương trình dạng y = ax² + b

Có: \(\left\{ \begin{array}{l}B = \left( {\frac{9}{2};0} \right) \in \left( P \right)\\D = \left( { - 4;1,6} \right) \in \left( P \right)\end{array} \right.\)

⇔ \(\left\{ \begin{array}{l}0 = a.{\left( {\frac{9}{2}} \right)^2} + b\\1,6 = a.{\left( { - 4} \right)^2} + b\end{array} \right.\)

⇔\(\left\{ \begin{array}{l}a = \frac{{ - 32}}{{85}}\\b = \frac{{648}}{{85}}\end{array} \right.\)

Tung độ ứng với hoành độ bằng 0 là y = a.0² + b = \(\frac{{648}}{{85}}\)

Vậy chiều cao của cổng Parabol là \(\frac{{648}}{{85}} \approx 7,6m.\)