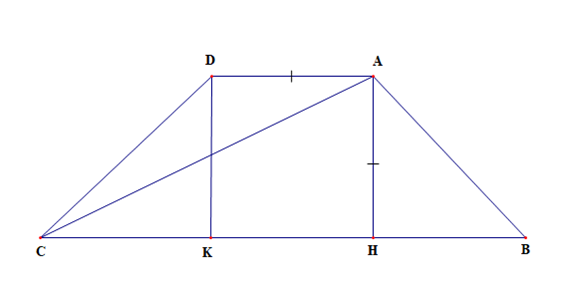
Gọi H, K là chân đường cao hạ từ A, D xuống BC

Khi đó tam giác ABH vuông tại H

Mà \(\widehat {ABC} = 45^\circ \)

Suy ra tam giác ABH vuông cân tại H

Do đó AH = BH = 2a

Vì hình thang ABCD cân

Nên AB = CD, \(\widehat {ABC} = \widehat {DCB}\), BD = AC

Xét tam giác ABH và tam giác DCK có

\(\widehat {AHB} = \widehat {DKC}\left( { = 90^\circ } \right)\)

AB = CD

\(\widehat {ABC} = \widehat {DCB}\)

Suy ra ∆ABH = ∆DCK (cạnh huyền – góc nhọn)

Do đó CK = BH = 2a

Ta có CH = AD + CK = 2a + 2a = 4a

Xét tam giac AHC vuông tại H có

AC² = AH² + CH²

Suy ra \[{\rm{AC = }}\sqrt {{{\left( {2{\rm{a}}} \right)}^2} + {{\left( {4{\rm{a}}} \right)}^2}} = 2{\rm{a}}\sqrt 5 \]

Ta có:

\(\left| {\overrightarrow {CB} - \overrightarrow {A{\rm{D}}} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {CB} + \overrightarrow {DA} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {CB} + \overrightarrow {DC} } \right| = \left| {\overrightarrow {DB} } \right| = AC = 2{\rm{a}}\sqrt 5 \)

Vậy ta chọn đáp án B.