Cho tam giác ABC có \(\widehat A = 120^\circ ,\) AB = AC = a. Quay tam giác ABC (bao gồm điểm trong tam giác) quanh đường thẳng AB ta được một khối tròn xoay. Thể tích khối tròn xoay đó bằng:
Cho tam giác ABC có \(\widehat A = 120^\circ ,\) AB = AC = a. Quay tam giác ABC (bao gồm điểm trong tam giác) quanh đường thẳng AB ta được một khối tròn xoay. Thể tích khối tròn xoay đó bằng:
A. \(\frac{{\pi {a^3}}}{3}.\)
B. \(\frac{{\pi {a^3}}}{4}.\)
C. \(\frac{{\pi {a^3}\sqrt 3 }}{2}.\)
D. \(\frac{{\pi {a^3}\sqrt 3 }}{4}.\)
Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: B
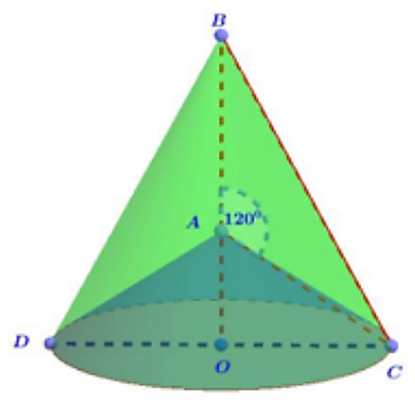
Quay tam giác ABC quanh đường thẳng AB ta được khối tròn xoay có thể tích V1, thể tích khối nón lớn có đỉnh B và thiết diện qua trục là BDC (hình vẽ) trừ đi V2 thể tích khối nón nhỏ có đỉnh A và thiết diện qua trục là ADC.
Gọi O là tâm đường tròn ngoại tiếp đáy của hai khối nón.
Xét tam giác AOC vuông tại O, có:
• \(\sin 60^\circ = \frac{{OC}}{{AC}}\) ⇒ \(OC = AC.\sin 60^\circ = \frac{{a\sqrt 3 }}{2}\)
• \(\cos 60^\circ = \frac{{AO}}{{AC}}\) ⇒ \(OA = AC.\cos 60^\circ = \frac{a}{2}\) ⇒ \(OB = \frac{{3a}}{2}.\)
Do đó \(V = {V_1} - {V_2} = \frac{1}{3}BO\,.\,\pi \,.\,O{C^2} - \frac{1}{3}OA\,.\,\pi \,.\,O{C^2}\)
\( = \frac{1}{3}\pi \,.\,O{C^2}\,\,.\,\,\left( {BO - OA} \right) = \frac{1}{3}\pi \,.\,{\left( {\frac{{a\sqrt 3 }}{2}} \right)^2}\,.\,a = \frac{{\pi {a^3}}}{4}.\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
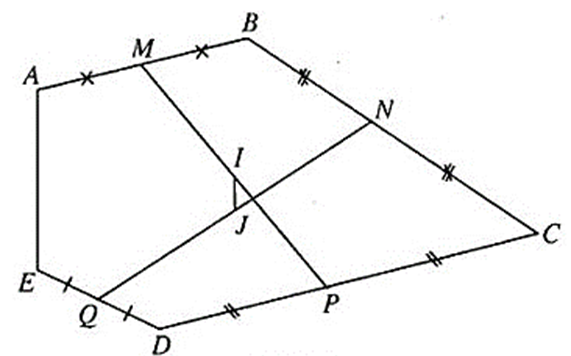
Ta có: \(2\overrightarrow {IJ} = \overrightarrow {IQ} + \overrightarrow {IN} = \overrightarrow {IM} + \overrightarrow {MQ} + \overrightarrow {IP} + \overrightarrow {PN} = \overrightarrow {MQ} + \overrightarrow {PN} \)
\( = \frac{1}{2}\left( {\overrightarrow {AE} + \overrightarrow {BD} } \right) + \frac{1}{2}\overrightarrow {DB} = \frac{1}{2}\overrightarrow {AE} \)
Do đó: \(\overrightarrow {IJ} = \frac{1}{4}\overrightarrow {AE} \) ⇒ \(4\overrightarrow {IJ} = \overrightarrow {AE} .\)
Vậy IJ // AE và 4IJ = AE.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
ĐK: x > 0.
\(\log _2^2x - 2{\log _2}\left( {2x} \right) - 1 = 0\) ⇔ \(\log _2^2x - 2{\log _2}2 - 2{\log _2}x - 1 = 0\)
⇔ \(\log _2^2x - 2{\log _2}x - 3 = 0\) (*)
Đặt log2x = t. Khi đó ta có:
(*) ⇔ \({t^2} - 2t - 3 = 0\) ⇔ (t + 1)(t – 3) = 0
⇔ \(\left[ {\begin{array}{*{20}{c}}{t + 1 = 0}\\{t - 3 = 0}\end{array}} \right.\) ⇔ \(\left[ {\begin{array}{*{20}{c}}{t = - 1}\\{t = 3}\end{array}} \right.\) ⇔ \(\left[ {\begin{array}{*{20}{c}}{{{\log }_2}x = - 1}\\{{{\log }_2}x = 3}\end{array}} \right.\)
⇔ \(\left[ {\begin{array}{*{20}{c}}{x = {2^{ - 1}} = \frac{1}{2}\left( {tm} \right)}\\{x = {2^3} = 8\left( {tm} \right)}\end{array}} \right.\)
⇒ \({x_1}{x_2} = \frac{1}{2}.8 = 4.\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. -2a2.
B. a2.
C. 2a2.
D. \( - \frac{{{a^2}}}{{\sqrt 2 }}.\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập