Vẽ trên cùng một mặt phẳng tọa độ Oxy đồ thị của các hàm số sau: y = ( frac{{ - 1}}{2}x ) (d1) và y = ( frac{1}{2}x ) + 3 (d2). Xác định b để đường thẳng (d3) y = 2x + b cắt (d2) tại điểm có tung độ...

+) Vẽ đồ thị hàm số (d1): y = ( frac{{ - 1}}{2}x ) Với x = 0 ⇒ y = 0 ta có điểm (0;0)( Với x = 2 ⇒ y = ( frac{{ - 1}}{2} ).2 = −1 ta có điểm (2;−1) Vẽ đường thẳng đi qua hai điểm (0;0);(2;−1) ta được (d1) +) Vẽ đồ thị hàm số (d2):y = ( frac{1}{2}x )+ 3 Với x = 0 ⇒ y = 3 ta có điểm (0;3) Với y = 0 ⇒ ( frac{1}{2}x )+ 3 = 0 ⇒ x = −6 ta có điểm (−6;0) Vẽ đường thẳng đi qua hai điểm (0;3);(−6;0) ta được (d2) Phương trình hoành độ giao điểm của (d3): y = 2x + b và (d2): y = ( frac{1}{2}x )+ 3 2x + b = ( frac{1}{2}x )+ 3 ⇔ ( frac{3}{2}x = 3 - b ) ⇔ x = (2 - frac{2}{3}b ) Thay x = (2 - frac{2}{3}b ) vào (d2) ta được: y = ( frac{1}{2} left( {2 - frac{2}{3}b} right) + 3 = 4 - frac{1}{3}b ) Vì giao điểm của (d2); (d3) có tung độ và hoành độ đối nhau ⇒ x + y = 0 ⇔ (2 - frac{2}{3}b + 4 - frac{1}{3}b = 0 ) ⇔ –b = – 6 ⇔ b = 6 Vậy b = 6.

Câu hỏi:

19/08/2025 2,851

Vẽ trên cùng một mặt phẳng tọa độ Oxy đồ thị của các hàm số sau:

y =\(\frac{{ - 1}}{2}x\) (d₁) và y = \(\frac{1}{2}x\) + 3 (d₂).

Xác định b để đường thẳng (d₃) y = 2x + b cắt (d₂) tại điểm có tung độ và hoành độ đối nhau.

Xem lời giải

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

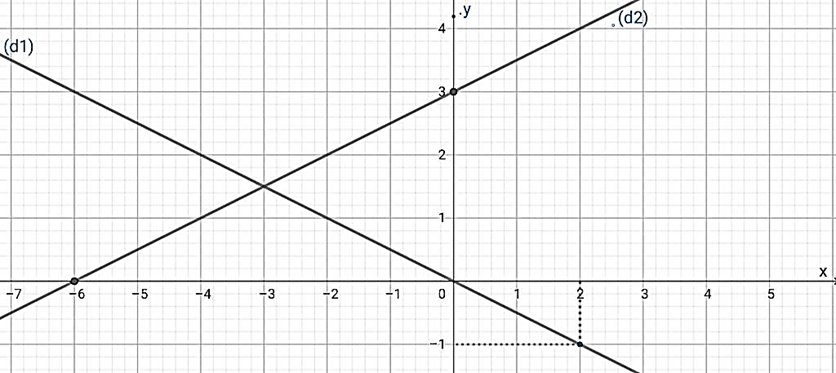
+) Vẽ đồ thị hàm số (d₁): y = \(\frac{{ - 1}}{2}x\)

Với x = 0 ⇒ y = 0 ta có điểm (0;0)(

Với x = 2 ⇒ y = \(\frac{{ - 1}}{2}\).2 = −1 ta có điểm (2;−1)

Vẽ đường thẳng đi qua hai điểm (0;0);(2;−1) ta được (d₁)

+) Vẽ đồ thị hàm số (d₂):y =\(\frac{1}{2}x\)+ 3

Với x = 0 ⇒ y = 3 ta có điểm (0;3)

Với y = 0 ⇒\(\frac{1}{2}x\)+ 3 = 0 ⇒ x = −6 ta có điểm (−6;0)

Vẽ đường thẳng đi qua hai điểm (0;3);(−6;0) ta được (d₂)

Vẽ trên cùng một mặt phẳng tọa độ Oxy đồ thị của các hàm số sau: y = -1/2 x (ảnh 1)

Phương trình hoành độ giao điểm của (d₃): y = 2x + b và (d₂): y =\(\frac{1}{2}x\)+ 3

2x + b = \(\frac{1}{2}x\)+ 3

⇔ \(\frac{3}{2}x = 3 - b\)

⇔ x = \(2 - \frac{2}{3}b\)

Thay x = \(2 - \frac{2}{3}b\) vào (d₂) ta được: y = \(\frac{1}{2}\left( {2 - \frac{2}{3}b} \right) + 3 = 4 - \frac{1}{3}b\)

Vì giao điểm của (d₂); (d₃) có tung độ và hoành độ đối nhau

⇒ x + y = 0

⇔ \(2 - \frac{2}{3}b + 4 - \frac{1}{3}b = 0\)

⇔ –b = – 6

⇔ b = 6

Vậy b = 6.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho ΔABC vuông tại A. Kẻ BD là tia phân giác của \(\widehat {ABC}\)(D ∈ AC). Trên cạnh BC lấy điểm E sao cho BE = BA.

a) Chứng minh ΔABD = ΔEBD.

b) Chứng minh: DE = AD và DE vuông góc với BC.

c) Chứng minh: BD là đường trung trực của đoạn AE.

d) Trên tia đối của tia AB lấy điểm F sao cho AF = CE. Chứng minh ba điểm F, D, E thẳng hàng.

Xem đáp án

Lời giải

Cho tam giác ABC vuông tại A. Kẻ BD là tia phân giác của góc ABC (D thuộc AC) (ảnh 1)

a) Xét tam giác ABD và tam giác EBD có:

AB = BE(gt)

\(\widehat {ABD} = \widehat {EBD}\)(do BD là phân giác \(\widehat {ABD}\))

Cạnh BD chung

Suy ra ΔABD = ΔEBD (c−g−c).

b) Theo câu a) ta có ΔABD = ΔEBD(c−g−c)

Nên DE = AD (hai cạnh tương ứng) và \(\widehat {BED} = \widehat {BAD} = 90^\circ \)(hai góc tương ứng)

Do đó: DE ⊥ BC.

c) Gọi I là giao điểm của BD và AE.

Xét tam giác ABI và tam giác EBI có:

AB = BE (gt)

\(\widehat {ABD} = \widehat {EBD}\) (do BD là phân giác \(\widehat {ABD}\))

Cạnh BI chung

Suy ra ΔABI = ΔEBI (c−g−c).

⇒ IA = IE, \(\widehat {BIA} = \widehat {BIE}\)

Mà \(\widehat {BIA} + \widehat {BIE} = 180^\circ \)(hai góc kề bù)

Nên \(\widehat {BIA} = \widehat {BIE} = 90^\circ \)

Hay BI ⊥ AE

Từ đó ta có BD ⊥ AE tại I và I là trung điểm AE.

Suy ra BD là đường trung trực của đoạn AE.

d) Theo câu b) ta có AD = DE

Xét tam giác ADF và tam giác EDC có:

AD = DE(cmt)

\(\widehat {FAD} = \widehat {DEC} = 90^\circ \)

AF = CE(gt)

Suy ra ΔADF = ΔEDC (c−g−c)

⇒ \(\widehat {ADF} = \widehat {CDF}\)

Mà A, D, C thẳng hàng nên suy ra F, D, E thẳng hàng.

Câu 2

Phép cộng, trừ 2 số cùng số mũ.

Xem đáp án

Lời giải

Không có công thức về cộng, trừ lũy thừa, ta thực hiện phép tính lũy thừa sau đó thực hiện cộng, trừ thông thường.

Ví dụ: 3² – 2² = 9 – 4 = 5

3² – 2² ≠ (3 – 2)² = 1.

Câu 3