Câu hỏi:
18/08/2023 2,486
Cho đường tròn (O; R) đường kính AB. Điểm C thuộc đường tròn sao cho AC > CB, C khác A và B. Kẻ CH vuông góc với AB tại H; kẻ OI vuông góc với AC tại I.
a) Chứng minh 4 điểm C, H, O, I cùng thuộc một đường tròn.
b) Kẻ tiếp tuyến Ax của đường tròn (O; R), tia OI cắt Ax tại M, chứng minh OI.OM = R2. Tính độ dài đoạn thẳng OI biết OM = 2R và R = 6cm.
Cho đường tròn (O; R) đường kính AB. Điểm C thuộc đường tròn sao cho AC > CB, C khác A và B. Kẻ CH vuông góc với AB tại H; kẻ OI vuông góc với AC tại I.
a) Chứng minh 4 điểm C, H, O, I cùng thuộc một đường tròn.
b) Kẻ tiếp tuyến Ax của đường tròn (O; R), tia OI cắt Ax tại M, chứng minh OI.OM = R2. Tính độ dài đoạn thẳng OI biết OM = 2R và R = 6cm.
Quảng cáo
Trả lời:
Giải bởi Vietjack
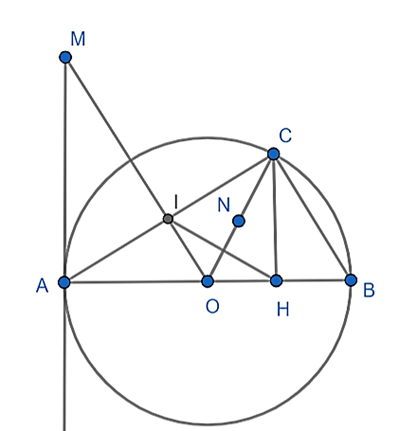
a) Gọi N là trung điểm của OC
Ta có: ΔOHC vuông tại H (CH⊥AB tại H)
Mà HN là đường trung tuyến ứng với cạnh huyền OC(N là trung điểm của OC)
Nên HN = \(\frac{{OC}}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
Mà ON = CN = \(\frac{{OC}}{2}\)(N là trung điểm của OC)
Nên HN = ON = CN (1)
Ta có: ΔOCI vuông tại I (OI ⊥ AC tại I)
Mà IN là đường trung tuyến ứng với cạnh huyền OC(N là trung điểm của OC)
Nên IN = \(\frac{{OC}}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
Mà CN = ON = \(\frac{{OC}}{2}\)(N là trung điểm của CO)
Nên IN = CN = ON (2)
Từ (1) và (2) suy ra NI = NO = NC = NH
Hay I,O,C,H cùng thuộc một đường tròn (đpcm)
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔMAO vuông tại A có AI là đường cao ứng với cạnh huyền OM, ta được:
OI.OM = OA2 mà OA = R (A ∈ (O;R))
nên OI.OM = R2 (đpcm)
Vì OM = 2R và R = 6cm nên OM = 2.6 = 12 (cm)
Thay OM = 12cm và R=6cm vào biểu thức OI.OM = R2, ta được:
OI⋅12 = 62 = 36
hay OI = 3 cm
Vậy: Khi OM = 2R và R = 6cm thì OI = 3cm.
Sách thầy cô Vietjack biên soạn
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho ΔABC vuông tại A. Kẻ BD là tia phân giác của \(\widehat {ABC}\)(D ∈ AC). Trên cạnh BC lấy điểm E sao cho BE = BA.
a) Chứng minh ΔABD = ΔEBD.
b) Chứng minh: DE = AD và DE vuông góc với BC.
c) Chứng minh: BD là đường trung trực của đoạn AE.
d) Trên tia đối của tia AB lấy điểm F sao cho AF = CE. Chứng minh ba điểm F, D, E thẳng hàng.
Cho ΔABC vuông tại A. Kẻ BD là tia phân giác của \(\widehat {ABC}\)(D ∈ AC). Trên cạnh BC lấy điểm E sao cho BE = BA.
a) Chứng minh ΔABD = ΔEBD.
b) Chứng minh: DE = AD và DE vuông góc với BC.
c) Chứng minh: BD là đường trung trực của đoạn AE.
d) Trên tia đối của tia AB lấy điểm F sao cho AF = CE. Chứng minh ba điểm F, D, E thẳng hàng.
Xem đáp án »
18/08/2023
106,689
Câu 3:
Có 3 bì thư giống nhau lần lượt được đánh số thứ tự từ 1 đến 3 và 3 con tem giống nhau lần lượt đánh số thứ tự từ 1 đến 3. Dán 3 con tem đó vào 3 bì thư sao cho không có bì thư nào không có tem. Tính xác suất để lấy ra được 2 bì thư trong 3 bì thư trên sao cho mỗi bì thư đều có số thứ tự giống với số thứ tự con tem đã dán vào nó.
Có 3 bì thư giống nhau lần lượt được đánh số thứ tự từ 1 đến 3 và 3 con tem giống nhau lần lượt đánh số thứ tự từ 1 đến 3. Dán 3 con tem đó vào 3 bì thư sao cho không có bì thư nào không có tem. Tính xác suất để lấy ra được 2 bì thư trong 3 bì thư trên sao cho mỗi bì thư đều có số thứ tự giống với số thứ tự con tem đã dán vào nó.
Xem đáp án »
18/08/2023
18,307
Câu 4:
Một cửa hàng nhập về 50 chiếc túi xách với giá góc 150 000 đồng/cái. Cửa hàng đã bán 30 chiếc với giá mỗi chiếc lãi 30% so với giá gốc, 20 chiếc còn lại bán lỗ 5% so với giá gốc. Hỏi sau khi bán hết 50 chiếc túi xách cửa hàng đó lãi hay lỗ bao nhiêu tiền?
Một cửa hàng nhập về 50 chiếc túi xách với giá góc 150 000 đồng/cái. Cửa hàng đã bán 30 chiếc với giá mỗi chiếc lãi 30% so với giá gốc, 20 chiếc còn lại bán lỗ 5% so với giá gốc. Hỏi sau khi bán hết 50 chiếc túi xách cửa hàng đó lãi hay lỗ bao nhiêu tiền?
Xem đáp án »
18/08/2023
12,987
Câu 6:
Cho tam giác ABC có ba góc nhọn và đường cao BE. Gọi H và K lần lượt là chân các đường vuông góc kẻ từ điểm E đến các đường thẳng AB và BC.
1) Chứng minh tứ giác BHEK là tứ giác nội tiếp.
2) Chứng minh: BH.BA = BK.BC.
3) Gọi F là chân đường vuông góc kẻ từ điểm C đến đường thẳng AB và I là trung điểm của đoạn thẳng EF. Chứng minh ba điểm H, I, K là ba điểm thẳng hàng.
Cho tam giác ABC có ba góc nhọn và đường cao BE. Gọi H và K lần lượt là chân các đường vuông góc kẻ từ điểm E đến các đường thẳng AB và BC.
1) Chứng minh tứ giác BHEK là tứ giác nội tiếp.
2) Chứng minh: BH.BA = BK.BC.
3) Gọi F là chân đường vuông góc kẻ từ điểm C đến đường thẳng AB và I là trung điểm của đoạn thẳng EF. Chứng minh ba điểm H, I, K là ba điểm thẳng hàng.
Xem đáp án »
18/08/2023
11,756
Câu 7:
Trên cùng phía của đường thẳng xy, vẽ 2 đường thằng AH và BK, sao cho AH vuông góc với xy ở H, BK vuông góc với xy ở K và BK = AH. Gọi O là trung điểm của đoạn HK. Chứng minh: \(\widehat {AOH} = \widehat {BOK}\).
Trên cùng phía của đường thẳng xy, vẽ 2 đường thằng AH và BK, sao cho AH vuông góc với xy ở H, BK vuông góc với xy ở K và BK = AH. Gọi O là trung điểm của đoạn HK. Chứng minh: \(\widehat {AOH} = \widehat {BOK}\).
Xem đáp án »
18/08/2023
10,574
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
80 câu Bài tập Hình học Khối đa diện có lời giải chi tiết (P1)
-
148 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu từ đề thi Đại học có lời giải (P1)
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
-
20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận