Câu hỏi:
18/08/2023 2,182
Cho đường tròn (O; R) đường kính AB, M là một điểm bất kì trên đường tròn (M khác A và B) tiếp tuyến cắt tại m cắt hai tiếp tuyến của A và B của đường tròn đã cho tại C và D. Chứng minh rằng: tứ giác AOMC và BOMD nội tiếp; \(\widehat {AOC} = \widehat {AMC} = \widehat {OBM} = \widehat {ODM}\).
Cho đường tròn (O; R) đường kính AB, M là một điểm bất kì trên đường tròn (M khác A và B) tiếp tuyến cắt tại m cắt hai tiếp tuyến của A và B của đường tròn đã cho tại C và D. Chứng minh rằng: tứ giác AOMC và BOMD nội tiếp; \(\widehat {AOC} = \widehat {AMC} = \widehat {OBM} = \widehat {ODM}\).
Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!
Bắt đầu thiQuảng cáo
Trả lời:
Giải bởi Vietjack
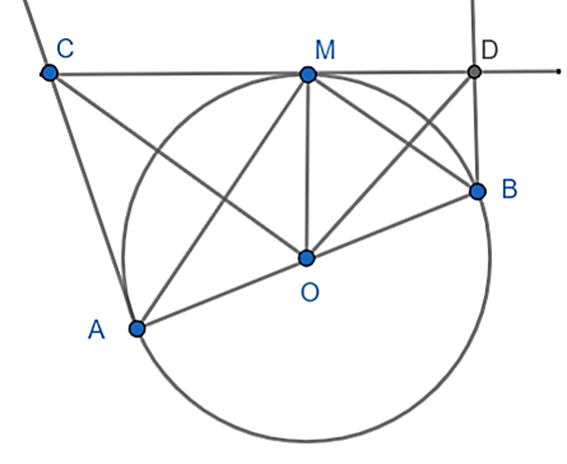
Xét tứ giác AOMC có
\(\widehat {OAC} = 90^\circ \) (tiếp tuyến của (O) tại A)
\(\widehat {OMC} = 90^\circ \)(tiếp tuyến của (O) tại M)
⇒ Tứ giác AOMC nội tiếp dường tròn đường kính OC (2 góc đối nhau có tổng =180 độ)
Xét tứ giác BOMD có
\(\widehat {OBD} = 90^\circ \)(tiếp tuyến của (O) tại B)
\(\widehat {OMD} = 90^\circ \)(tiếp tuyến của (O) tại M)
⇒ Tứ giác BOMD nội tiếp đường tròn đường kính OD (2 góc đối nhau có tổng bằng 180 độ)
Ta có : \(\widehat {OBM} = \widehat {AMC}\)(góc tạo bởi tia tiếp tuyến và dây cung, góc nội tiếp cùng chắn cung AM)
\(\widehat {AOC} = \widehat {AMC}\)(góc nội tiếp chắn cung AC của đường tròn ngoại tiếp tứ giác AOMC)
\(\widehat {OBM} = \widehat {ODM}\) (góc nội tiếp chắn cung OM của đường tròn ngoại tiếp tứ giác BOMD)
⇒ \(\widehat {AOC} = \widehat {AMC} = \widehat {OBM} = \widehat {ODM}\).
Nhà sách vietjack
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho ΔABC vuông tại A. Kẻ BD là tia phân giác của \(\widehat {ABC}\)(D ∈ AC). Trên cạnh BC lấy điểm E sao cho BE = BA.
a) Chứng minh ΔABD = ΔEBD.
b) Chứng minh: DE = AD và DE vuông góc với BC.
c) Chứng minh: BD là đường trung trực của đoạn AE.
d) Trên tia đối của tia AB lấy điểm F sao cho AF = CE. Chứng minh ba điểm F, D, E thẳng hàng.
Cho ΔABC vuông tại A. Kẻ BD là tia phân giác của \(\widehat {ABC}\)(D ∈ AC). Trên cạnh BC lấy điểm E sao cho BE = BA.
a) Chứng minh ΔABD = ΔEBD.
b) Chứng minh: DE = AD và DE vuông góc với BC.
c) Chứng minh: BD là đường trung trực của đoạn AE.
d) Trên tia đối của tia AB lấy điểm F sao cho AF = CE. Chứng minh ba điểm F, D, E thẳng hàng.
Xem đáp án »
18/08/2023
94,047
Câu 3:
Có 3 bì thư giống nhau lần lượt được đánh số thứ tự từ 1 đến 3 và 3 con tem giống nhau lần lượt đánh số thứ tự từ 1 đến 3. Dán 3 con tem đó vào 3 bì thư sao cho không có bì thư nào không có tem. Tính xác suất để lấy ra được 2 bì thư trong 3 bì thư trên sao cho mỗi bì thư đều có số thứ tự giống với số thứ tự con tem đã dán vào nó.
Có 3 bì thư giống nhau lần lượt được đánh số thứ tự từ 1 đến 3 và 3 con tem giống nhau lần lượt đánh số thứ tự từ 1 đến 3. Dán 3 con tem đó vào 3 bì thư sao cho không có bì thư nào không có tem. Tính xác suất để lấy ra được 2 bì thư trong 3 bì thư trên sao cho mỗi bì thư đều có số thứ tự giống với số thứ tự con tem đã dán vào nó.
Xem đáp án »
18/08/2023
15,949
Câu 4:
Một cửa hàng nhập về 50 chiếc túi xách với giá góc 150 000 đồng/cái. Cửa hàng đã bán 30 chiếc với giá mỗi chiếc lãi 30% so với giá gốc, 20 chiếc còn lại bán lỗ 5% so với giá gốc. Hỏi sau khi bán hết 50 chiếc túi xách cửa hàng đó lãi hay lỗ bao nhiêu tiền?
Một cửa hàng nhập về 50 chiếc túi xách với giá góc 150 000 đồng/cái. Cửa hàng đã bán 30 chiếc với giá mỗi chiếc lãi 30% so với giá gốc, 20 chiếc còn lại bán lỗ 5% so với giá gốc. Hỏi sau khi bán hết 50 chiếc túi xách cửa hàng đó lãi hay lỗ bao nhiêu tiền?
Xem đáp án »
18/08/2023
12,911
Câu 6:
Trên cùng phía của đường thẳng xy, vẽ 2 đường thằng AH và BK, sao cho AH vuông góc với xy ở H, BK vuông góc với xy ở K và BK = AH. Gọi O là trung điểm của đoạn HK. Chứng minh: \(\widehat {AOH} = \widehat {BOK}\).
Trên cùng phía của đường thẳng xy, vẽ 2 đường thằng AH và BK, sao cho AH vuông góc với xy ở H, BK vuông góc với xy ở K và BK = AH. Gọi O là trung điểm của đoạn HK. Chứng minh: \(\widehat {AOH} = \widehat {BOK}\).
Xem đáp án »
18/08/2023
10,507
Câu 7:
Cho tam giác ABC có ba góc nhọn và đường cao BE. Gọi H và K lần lượt là chân các đường vuông góc kẻ từ điểm E đến các đường thẳng AB và BC.
1) Chứng minh tứ giác BHEK là tứ giác nội tiếp.
2) Chứng minh: BH.BA = BK.BC.
3) Gọi F là chân đường vuông góc kẻ từ điểm C đến đường thẳng AB và I là trung điểm của đoạn thẳng EF. Chứng minh ba điểm H, I, K là ba điểm thẳng hàng.
Cho tam giác ABC có ba góc nhọn và đường cao BE. Gọi H và K lần lượt là chân các đường vuông góc kẻ từ điểm E đến các đường thẳng AB và BC.
1) Chứng minh tứ giác BHEK là tứ giác nội tiếp.
2) Chứng minh: BH.BA = BK.BC.
3) Gọi F là chân đường vuông góc kẻ từ điểm C đến đường thẳng AB và I là trung điểm của đoạn thẳng EF. Chứng minh ba điểm H, I, K là ba điểm thẳng hàng.
Xem đáp án »
18/08/2023
9,267
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)
-
124 câu Trắc nghiệm Ôn tập Toán 12 Chương 3 Hình học có đáp án (Phần 1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận