Cho dãy gồm 6 số nguyên tố phân biệt và tăng dần. Hiệu giữa hai số liên tiếp của dãy số đã cho đều bằng nhau. Chứng minh rằng hiệu giữa số lớn nhất và số bé nhất không nhỏ hơn 150.

Xem lời giải

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Gọi 6 số đó là p, p + d, p + 2d, p + 3d, p + 4d, p + 5d.

p + d, p + 2d là 2 số lẻ ⇒ hiệu ⋮ 2 (p + d ≥ 4)

p + d, p + 2d, p + 3d > 3 các số này ⋮̸ 3 nên có 2 số có cùng số dư khi chia 3.

Hiệu của chúng là d hoặc 2d ⋮ 3

⇒ d ⋮ 3

⇒ d ⋮ 6 nên d ≥ 6

p + d, p + 2d, p + 3d, p + 4d, p + 5d là 5 số, các số này không chia hết 5 nên có 2 số có cùng số dư khi chia 5.

Hiệu của chúng là d, 2d, 3d hoặc 4d ⋮ 5

⇒ d ⋮ 5

⇒ d ⋮ 30

Ta có : d ≥ 30

⇒ 5d ≥ 150 (đpcm)

Vậy hiệu giữa số lớn nhất và số bé nhất không nhỏ hơn 150.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một vận động viên bơi về phía Bắc với vận tốc 1,7 m/s. Nước sông chảy với vận tốc 1 m/s về phía Đông. Tính độ lớn và hướng vận tốc tổng hợp của vận động viên?

Xem đáp án

Lời giải

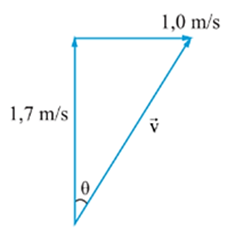
Một vận động viên bơi về phía Bắc với vận tốc 1,7 m/s. Nước sông chảy với vận tốc 1 (ảnh 1)

Độ lớn vận tốc tổng hợp của vận động viên là:

\(\overrightarrow v \)_{tổng hợp} = \(\overrightarrow v \) + \(\overrightarrow v \)_nước

Suy ra: v_{tổng hợp} = \(\sqrt {{v^2} + {v_{nuoc}}^2} = \sqrt {1,{7^2} + {1^2}} = 1,97\left( {m/s} \right)\)

Hướng vận tốc tổng hợp của vận động viên hợp với bờ sông 1 góc là:

\(\tan \alpha = \frac{v}{{{v_{nuoc}}}} = \frac{{1,7}}{1} = 1,7 \Rightarrow \alpha \approx 59,53^\circ \)

Câu 2

Hàm số y = f(x² + 2x) nghịch biến trên khoảng nào?

x

–∞

–2

1

3                    +∞

f'(x)

–

0           +

0             –

0            –

Xem đáp án

Lời giải

y = f(x² + 2x)

y' = (2x + 2)f'(x² + 2x)

Xét y' = 0 ta có: (2x + 2)f'(x² + 2x) = 0

⇒ \(\left[ \begin{array}{l}2x + 2 = 0\\f'\left( {{x^2} + 2x} \right) = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\\{x^2} + 2x = - 2\\{x^2} + 2x = 1\\{x^2} + 2x = 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 1\\x = - 3\\x = - 1 + \sqrt 2 \\x = - 1 - \sqrt 2 \end{array} \right.\)

Ta có bảng biến thiên:

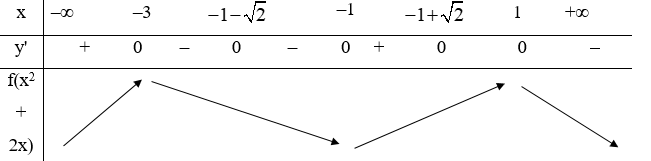
Hàm số y = f(x^2 + 2x) nghịch biến trên khoảng nào x - vô cùng -2 1 3 + vô cùng (ảnh 1)

Vậy hàm số nghịch biến trên (–3; –1) và (1; +∞)

Câu 3