Cho tam giác ABC có AB = 6 cm, AC = 9 cm, BC = 10 cm, đường phân giác trong AD, đường phân giác ngoài AE.

a) Tính DB, EB.

b) Chứng minh tam giác ADE vuông.

c) Tính tỉ số diện tích của tam giác ABD và tam giác ADC.

Xem lời giải

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Quảng cáo

Trả lời:

Giải bởi Vietjack

Cho tam giác ABC có AB = 6 cm, AC = 9 cm, BC = 10 cm, đường phân giác trong AD (ảnh 1)

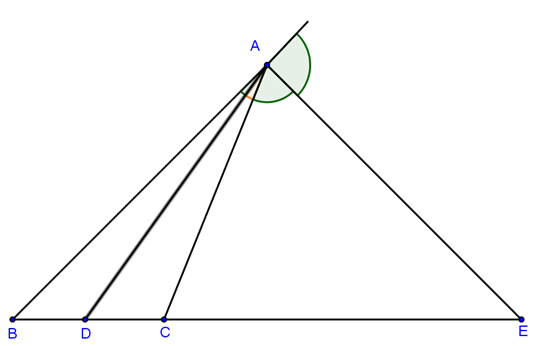
a) Theo tính chất đường phân giác ta có:

\(\frac{{DB}}{{AB}} = \frac{{DC}}{{AC}} = \frac{{DB + DC}}{{AB + AC}} = \frac{{BC}}{{AB + AC}} = \frac{{10}}{{15}} = \frac{2}{3}\)

Suy ra: DB = \(\frac{2}{3}AB = \frac{2}{3}.6 = 4\left( {cm} \right)\)

\(\frac{{EB}}{{AB}} = \frac{{EC}}{{AC}} = \frac{{EC - EB}}{{AC - AB}} = \frac{{BC}}{{AC - AB}} = \frac{{10}}{{9 - 6}} = \frac{{10}}{3}\)

⇒ EB = \(\frac{{10}}{3}.6 = 20\left( {cm} \right)\)

b) Vì AE và AD là phân giác của 2 góc kề bù

⇒ \(\widehat {EAD}\)vuông

⇒ Tam giác ADE vuông tại A

c) Ta có tam giác ABD và ADC có chung đường cao hạ từ đỉnh A nên tỉ số diện tích 2 tam giác chính là tỉ số giữa 2 cạnh đáy

Mà theo tính chất đường phân giác: \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\)

⇒ \(\frac{{{S_{ABD}}}}{{{S_{ADC}}}} = \frac{{DB}}{{DC}} = \frac{{AB}}{{AC}} = \frac{6}{9} = \frac{2}{3}\)

Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một vận động viên bơi về phía Bắc với vận tốc 1,7 m/s. Nước sông chảy với vận tốc 1 m/s về phía Đông. Tính độ lớn và hướng vận tốc tổng hợp của vận động viên?

Xem đáp án

Lời giải

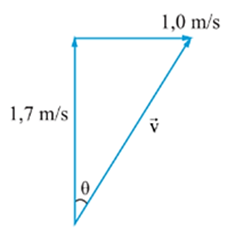
Một vận động viên bơi về phía Bắc với vận tốc 1,7 m/s. Nước sông chảy với vận tốc 1 (ảnh 1)

Độ lớn vận tốc tổng hợp của vận động viên là:

\(\overrightarrow v \)_{tổng hợp} = \(\overrightarrow v \) + \(\overrightarrow v \)_nước

Suy ra: v_{tổng hợp} = \(\sqrt {{v^2} + {v_{nuoc}}^2} = \sqrt {1,{7^2} + {1^2}} = 1,97\left( {m/s} \right)\)

Hướng vận tốc tổng hợp của vận động viên hợp với bờ sông 1 góc là:

\(\tan \alpha = \frac{v}{{{v_{nuoc}}}} = \frac{{1,7}}{1} = 1,7 \Rightarrow \alpha \approx 59,53^\circ \)

Câu 2

Hàm số y = f(x² + 2x) nghịch biến trên khoảng nào?

x

–∞

–2

1

3                    +∞

f'(x)

–

0           +

0             –

0            –

Xem đáp án

Lời giải

y = f(x² + 2x)

y' = (2x + 2)f'(x² + 2x)

Xét y' = 0 ta có: (2x + 2)f'(x² + 2x) = 0

⇒ \(\left[ \begin{array}{l}2x + 2 = 0\\f'\left( {{x^2} + 2x} \right) = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\\{x^2} + 2x = - 2\\{x^2} + 2x = 1\\{x^2} + 2x = 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 1\\x = - 3\\x = - 1 + \sqrt 2 \\x = - 1 - \sqrt 2 \end{array} \right.\)

Ta có bảng biến thiên:

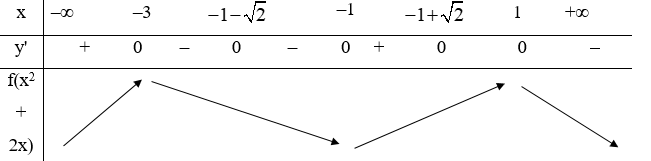
Hàm số y = f(x^2 + 2x) nghịch biến trên khoảng nào x - vô cùng -2 1 3 + vô cùng (ảnh 1)

Vậy hàm số nghịch biến trên (–3; –1) và (1; +∞)

Câu 3