Cho hình bình hành ABCD. Trên các cạnh AB và CD lần lượt lấy các điểm M và N sao cho AM = DN. Đường trung trực của BM lần lượt cắt các đường thẳng MN và BC tại E và F.

a) Chứng minh E và F đối xứng với nhau qua AB.

b) Chứng minh tứ giác MEBF là hình thoi.

c) Hình bình hành ABCD có thêm điều kiện gì để tứ giác BCNE là hình thang cân.

Xem lời giải

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

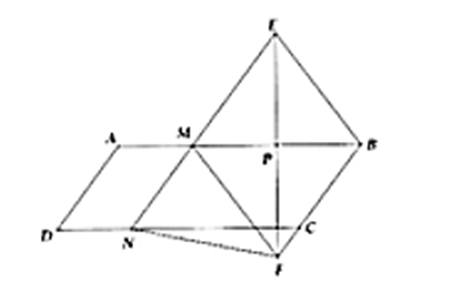
Cho hình bình hành ABCD. Trên các cạnh AB và CD lần lượt lấy các điểm M và N sao (ảnh 1)

a) Do AM = DN và AM // DN (do AB // CD)

⇒ MADN là hình bình hành

⇒ \(\widehat D = \widehat {AMN} = \widehat {EMB} = \widehat {MBC}\)

Xét ∆MPE và ∆BPE có:

Chung PE

\(\widehat {MPE} = \widehat {BPE}\)

MP = BP (EP là trung trực MB)

Ta có ∆MPE = ∆BPE nên EP = FP.

Vậy MEBF là hình thoi và 2 điểm E, F đối xứng nhau qua AB.

b) Tứ giác MEBF có MB ∩ EF = P;

Lại có P trung điểm BM, P là trung điểm EF, MB ^ EF.

⇒ MEBF là hình thoi.

c) Để BNCE là hình thang cân thì \(\widehat {CNE} = \widehat {BEN}\)

Mà \(\widehat {CNE} = \widehat D = \widehat {EMB} = \widehat {MBC}\)

nên DMEB có 3 góc bằng nhau, suy ra điều kiện để BNCE là hình thang cân thì \(\widehat {ABC} = 60^\circ \).

Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay

Các sản phẩm khác của Vietjack:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một vận động viên bơi về phía Bắc với vận tốc 1,7 m/s. Nước sông chảy với vận tốc 1 m/s về phía Đông. Tính độ lớn và hướng vận tốc tổng hợp của vận động viên?

Xem đáp án

Lời giải

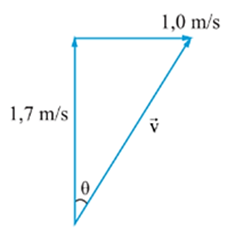
Một vận động viên bơi về phía Bắc với vận tốc 1,7 m/s. Nước sông chảy với vận tốc 1 (ảnh 1)

Độ lớn vận tốc tổng hợp của vận động viên là:

\(\overrightarrow v \)_{tổng hợp} = \(\overrightarrow v \) + \(\overrightarrow v \)_nước

Suy ra: v_{tổng hợp} = \(\sqrt {{v^2} + {v_{nuoc}}^2} = \sqrt {1,{7^2} + {1^2}} = 1,97\left( {m/s} \right)\)

Hướng vận tốc tổng hợp của vận động viên hợp với bờ sông 1 góc là:

\(\tan \alpha = \frac{v}{{{v_{nuoc}}}} = \frac{{1,7}}{1} = 1,7 \Rightarrow \alpha \approx 59,53^\circ \)

Câu 2

Hàm số y = f(x² + 2x) nghịch biến trên khoảng nào?

x

–∞

–2

1

3                    +∞

f'(x)

–

0           +

0             –

0            –

Xem đáp án

Lời giải

y = f(x² + 2x)

y' = (2x + 2)f'(x² + 2x)

Xét y' = 0 ta có: (2x + 2)f'(x² + 2x) = 0

⇒ \(\left[ \begin{array}{l}2x + 2 = 0\\f'\left( {{x^2} + 2x} \right) = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\\{x^2} + 2x = - 2\\{x^2} + 2x = 1\\{x^2} + 2x = 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 1\\x = - 3\\x = - 1 + \sqrt 2 \\x = - 1 - \sqrt 2 \end{array} \right.\)

Ta có bảng biến thiên:

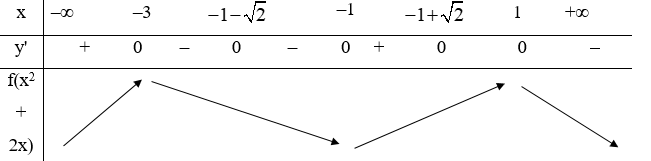
Hàm số y = f(x^2 + 2x) nghịch biến trên khoảng nào x - vô cùng -2 1 3 + vô cùng (ảnh 1)

Vậy hàm số nghịch biến trên (–3; –1) và (1; +∞)

Câu 3