Cho tam giác ABC hãy chỉ ra vị trí của điểm M thỏa mãn mỗi trường hợp sau đây:

a) \(\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow {BA} \).

b) \(\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \).

Xem lời giải

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

a) \(\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow {BA} \)

⇔ \[\overrightarrow {MA} + \overrightarrow {BM} + \overrightarrow {MC} = \overrightarrow {BA} \]

⇔ \[\overrightarrow {BA} + \overrightarrow {MC} = \overrightarrow {BA} \]

⇔ \[\overrightarrow {MC} = \overrightarrow 0 \]

Suy ra: M trùng với C

b) \(\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \)

⇔ \(\overrightarrow {BA} + \overrightarrow {MC} = \overrightarrow 0 \)

⇔ \(\overrightarrow {BA} = - \overrightarrow {MC} = \overrightarrow {CM} \)

Vậy M là đỉnh còn lại của hình bình hành ABCM.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một vận động viên bơi về phía Bắc với vận tốc 1,7 m/s. Nước sông chảy với vận tốc 1 m/s về phía Đông. Tính độ lớn và hướng vận tốc tổng hợp của vận động viên?

Xem đáp án

Lời giải

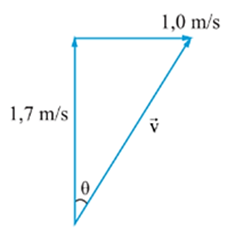
Một vận động viên bơi về phía Bắc với vận tốc 1,7 m/s. Nước sông chảy với vận tốc 1 (ảnh 1)

Độ lớn vận tốc tổng hợp của vận động viên là:

\(\overrightarrow v \)_{tổng hợp} = \(\overrightarrow v \) + \(\overrightarrow v \)_nước

Suy ra: v_{tổng hợp} = \(\sqrt {{v^2} + {v_{nuoc}}^2} = \sqrt {1,{7^2} + {1^2}} = 1,97\left( {m/s} \right)\)

Hướng vận tốc tổng hợp của vận động viên hợp với bờ sông 1 góc là:

\(\tan \alpha = \frac{v}{{{v_{nuoc}}}} = \frac{{1,7}}{1} = 1,7 \Rightarrow \alpha \approx 59,53^\circ \)

Câu 2

Hàm số y = f(x² + 2x) nghịch biến trên khoảng nào?

x

–∞

–2

1

3                    +∞

f'(x)

–

0           +

0             –

0            –

Xem đáp án

Lời giải

y = f(x² + 2x)

y' = (2x + 2)f'(x² + 2x)

Xét y' = 0 ta có: (2x + 2)f'(x² + 2x) = 0

⇒ \(\left[ \begin{array}{l}2x + 2 = 0\\f'\left( {{x^2} + 2x} \right) = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\\{x^2} + 2x = - 2\\{x^2} + 2x = 1\\{x^2} + 2x = 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 1\\x = - 3\\x = - 1 + \sqrt 2 \\x = - 1 - \sqrt 2 \end{array} \right.\)

Ta có bảng biến thiên:

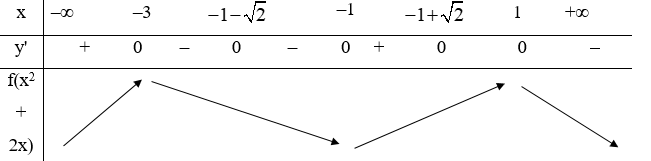
Hàm số y = f(x^2 + 2x) nghịch biến trên khoảng nào x - vô cùng -2 1 3 + vô cùng (ảnh 1)

Vậy hàm số nghịch biến trên (–3; –1) và (1; +∞)

Câu 3