Cho hình chóp S.ABCD có đáy là hình thoi cạnh a, \[\widehat {BAD} = 60^\circ ,\] SA = a và SA vuông góc với mặt phẳng đáy. Khoảng cách từ B đến mặt phẳng (SCD) bằng:
Cho hình chóp S.ABCD có đáy là hình thoi cạnh a, \[\widehat {BAD} = 60^\circ ,\] SA = a và SA vuông góc với mặt phẳng đáy. Khoảng cách từ B đến mặt phẳng (SCD) bằng:
A. \(\frac{{\sqrt {21} a}}{7}\)
B. \(\frac{{\sqrt {15} a}}{7}\)
C. \(\frac{{\sqrt {21} a}}{3}\)
D. \(\frac{{\sqrt {15} a}}{3}\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: A
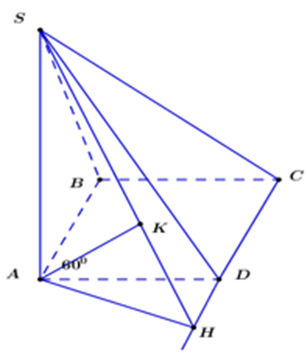
Ta có: AB // (SCD)
⇒ d(B; (SCD)) = d(A; (SCD)) = d
Kẻ AH ⊥ CD; AK ⊥ SH
\(\left\{ {\begin{array}{*{20}{c}}{CD \bot SA}\\{CD \bot AH}\end{array} \Rightarrow CD \bot \left( {SAH} \right)} \right.\)
⇒ CD ⊥ AK ⇒ AK ⊥ (SCD)
⇒ d(B; (SCD)) = d = AK.
Xét ∆AHD vuông tại H, \[\widehat {ADH} = 60^\circ \]
ta có: \(AH = AD \cdot {\rm{sin}}60^\circ = \frac{{a\sqrt 3 }}{2}\)
Áp dụng hệ thức lượng trong tam giác vuông SHA vuông tại A có đường cao AK ta có: \(AK = \frac{{SA \cdot AH}}{{\sqrt {S{A^2} + A{H^2}} }}\)\( = \frac{{a \cdot \frac{{a\sqrt 3 }}{2}}}{{\sqrt {{a^2} + \frac{{3{a^2}}}{4}} }} = \frac{{a\sqrt {21} }}{7} = d.\)
Hot: Danh sách các trường đã công bố điểm chuẩn Đại học 2025 (mới nhất) (2025). Xem ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \[x = - \frac{\pi }{2} + k2\pi .\]
B. \[x = \frac{\pi }{2} + k\pi .\]
C. \[x = k\pi .\]
D. \[x = \frac{\pi }{2} + k2\pi .\]
Lời giải
Đáp án đúng là: D
Sin x = 1 ⇔ \[x = \frac{\pi }{2} + k2\pi .\]
Câu 2
A. a = 2.
B. b = 1.
C. b = 2.
D. c = 1.
Lời giải
Đáp án đúng là: D
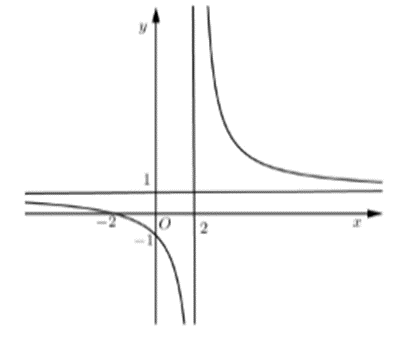
Ta có đồ thị hàm số \[y = \frac{{ax + 2}}{{cx + b}}\] đi qua điểm có tọa độ (0; −1)
Thay x = 0; y = −1 vào hàm số ta được \[ - 1 = \frac{{a \cdot 0 + 2}}{{c \cdot 0 + b}} \Rightarrow b = - 2.\]
Đồ thị hàm số \[y = \frac{{ax + 2}}{{cx - 2}}\]có ⇒ a = 1; b = −2; c = 1
Đáp án cần chọn là: D.
Câu 3
A. (−∞; 2].
B. [2; +∞).
C. (−∞; 2).
D. (2; +∞).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \( - \frac{3}{2}.\)
B. 1.
C. \( - \frac{1}{2}.\)
D. \(\frac{1}{2}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(\frac{{16}}{9}.\)
B. \(\frac{{14}}{9}.\)
C. \(\frac{{25}}{9}.\)
D. 1.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. m = ‒3.
B. m = 3.
C. m = 4.
D. m = ‒4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo