Một bình đựng 5 viên bi xanh và 3 viên bi đỏ (các viên bi chỉ khác nhau về màu sắc). Lấy ngẫu nhiên một viên bi, rồi lấy ngẫu nhiên một viên bi nữa. Khi tính xác suất của biến cố “Lấy lần thứ hai được một viên bi xanh”, ta được kết quả:
Một bình đựng 5 viên bi xanh và 3 viên bi đỏ (các viên bi chỉ khác nhau về màu sắc). Lấy ngẫu nhiên một viên bi, rồi lấy ngẫu nhiên một viên bi nữa. Khi tính xác suất của biến cố “Lấy lần thứ hai được một viên bi xanh”, ta được kết quả:
A.\(\frac{5}{8}\)
B.\(\frac{5}{9}\)
C.\(\frac{5}{7}\)
D.\(\frac{4}{7}\).
Quảng cáo
Trả lời:
Đáp án đúng là: A
Gọi A là biến cố “Lấy lần thứ hai được một viên bi xanh”. Có hai trường hợp xảy ra
Biến cố B: Lấy lần thứ nhất được bi xanh, lấy lần thứ hai cũng được một bi xanh
Xác suất trong trường hợp này là \({P_B} = \frac{5}{8}.\frac{4}{7} = \frac{5}{{14}}\)
Biến cố C: Lấy lần thứ nhất được bi đỏ, lấy lần thứ hai được bi xanh
Xác suất trong trường hợp này là \({P_C} = \frac{3}{8}.\frac{5}{7} = \frac{{15}}{{56}}\)
Ta thấy 2 biến cố B và C là xung khắc nên \({P_A} = {P_B} + {P_C} = \frac{5}{{14}} + \frac{{15}}{{56}} = \frac{5}{8}\)
Vậy ta chọn đáp án A.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: D
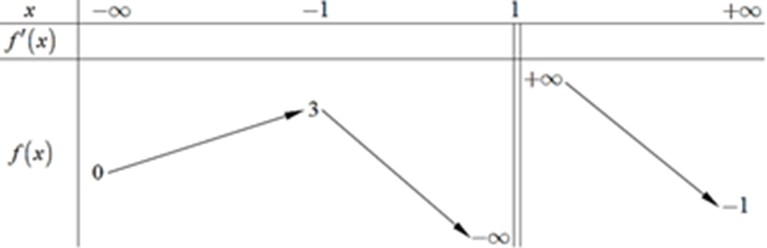
Ta có sô nghiệm của phương trình f(x) = m bằng số giao điềm của đồ thị hàm số y = f(x) và đường thẳng y = m
Do đó, dựa vào bàng biến thiên ta thấy, phương trình f(x) = m có 3 nghiệm phân biệt khi và chỉ khi 0 < m < 3
Kết hợp điều kiện \(m \in \mathbb{Z}\) suy ra \(m \in \{ 1;2\} \)
Do đó có 2 giá trị nguyên của tham số m thòa mãn yêu cầu bài toán
Vậy ta chọn đáp án D.
Lời giải
Đặt \(f(x) = {x^2} - 4x + m\)
Để phương trình có 2 nghiệm thỏa mãn \(0 < {x_1} < {x_2} < 3\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\Delta ' > 0}\\{f(0) > 0}\\{f(3) > 0}\\{0 < \frac{S}{2} < 3}\end{array} \Leftrightarrow \left\{ \begin{array}{l}{4^2} - 4m > 0\\0 + m > 0\\{3^2} - 4.3 + m > 0\\0 < \frac{4}{2} < 3\end{array} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{4 - m > 0}\\{m > 0}\\{m - 3 > 0}\\{0 < 2 < 3}\end{array} \Leftrightarrow 3 < m < 4} \right.} \right.\)
Vậy 3 < m < 4.
Câu 3
A. m ≥ f(1) – e
B. \(m > f\left( { - 1} \right) - \frac{1}{e}\)
C. \(m \ge f\left( { - 1} \right) - \frac{1}{e}\)
D. m > f(1) – e .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. G = 1
B. \(G = \frac{{ - 4}}{5}\)
C. \(G = \frac{{ - 6}}{5}\)
D. G = –1.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. 665 280
B. 85 680
C. 119
D. 579 600.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.