Cho hình chóp S.ABCD có đáy ABCD là hình thang có đáy lớn BC, đáy nhỏ AD. Mặt bên (SAD) là tam giác đều, (α) là mặt phẳng đi qua M trên cạnh AB, song song với SA, BC. Mp (α) cắt các cạnh CD, SC, SB lần lượt tại N, P, Q. Tứ giác MNPQ là hình gì?
Cho hình chóp S.ABCD có đáy ABCD là hình thang có đáy lớn BC, đáy nhỏ AD. Mặt bên (SAD) là tam giác đều, (α) là mặt phẳng đi qua M trên cạnh AB, song song với SA, BC. Mp (α) cắt các cạnh CD, SC, SB lần lượt tại N, P, Q. Tứ giác MNPQ là hình gì?
A. Hình thoi
B. Hình bình hành
C. Tứ giác có các cạnh đối cắt nhau
D. Hình thang cân.
Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: D
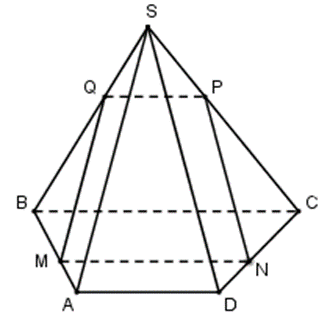
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{BC\,{\rm{//}}\,(\alpha ),BC \subset (ABCD),BC \subset (SBC)}\\{(\alpha ) \cap (ABCD) = MN}\\{(\alpha ) \cap (SBC) = PQ}\end{array}} \right. \Rightarrow MN\,{\rm{//}}\,BC\,{\rm{//}}\,PQ\quad \)
Suy ra tứ giác MNPQ là hình thang (1)
Vì \(\left\{ {\begin{array}{*{20}{l}}{(\alpha ) \cap (SAB) = MQ}\\{(\alpha )\,{\rm{//}}\,SA,SA \subset (SAB)}\end{array} \Rightarrow SA\,{\rm{//}}\,MQ} \right.\)
Áp dụng định lý Ta – lét ta có:
\(\begin{array}{l}\frac{{AM}}{{AB}} = \frac{{SQ}}{{SB}} = \frac{{SP}}{{SC}};\frac{{AM}}{{AB}} = \frac{{DN}}{{DC}}\\ \Rightarrow \frac{{SP}}{{SC}} = \frac{{DN}}{{DC}} \Rightarrow NP\,{\rm{//}}\,SD\end{array}\)
Vì \(\left\{ {\begin{array}{*{20}{l}}{MQ\,{\rm{//}}\,SA}\\{MN\,{\rm{//}}\,BC\,{\rm{//}}\,AD}\end{array} \Rightarrow \widehat {NMQ} = \widehat {SAD}} \right.{\rm{ }}\)
Mà tam giác SAD đều nên \(\widehat {SA{\rm{D}}} = 60^\circ \)
Suy ra \(\widehat {NMQ} = 60^\circ \)
Chứng minh tương tự ta có \(\widehat {MNP} = \widehat {SDA} = 60^\circ \)
Do đó \(\widehat {NMQ} = \widehat {MNP}\) (2)
Từ (1) và (2) suy ra MNPQ là hình thang cân
Vậy đáp án cần chọn là: D.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi cuối kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: D
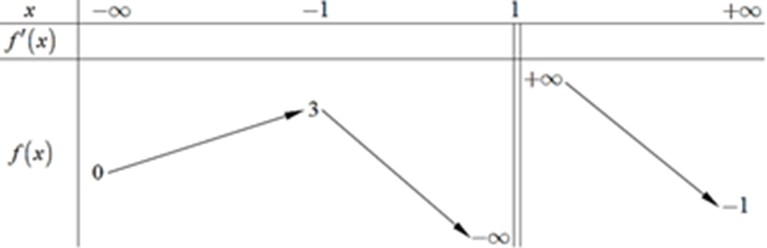
Ta có sô nghiệm của phương trình f(x) = m bằng số giao điềm của đồ thị hàm số y = f(x) và đường thẳng y = m
Do đó, dựa vào bàng biến thiên ta thấy, phương trình f(x) = m có 3 nghiệm phân biệt khi và chỉ khi 0 < m < 3
Kết hợp điều kiện \(m \in \mathbb{Z}\) suy ra \(m \in \{ 1;2\} \)
Do đó có 2 giá trị nguyên của tham số m thòa mãn yêu cầu bài toán
Vậy ta chọn đáp án D.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đặt \(f(x) = {x^2} - 4x + m\)
Để phương trình có 2 nghiệm thỏa mãn \(0 < {x_1} < {x_2} < 3\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\Delta ' > 0}\\{f(0) > 0}\\{f(3) > 0}\\{0 < \frac{S}{2} < 3}\end{array} \Leftrightarrow \left\{ \begin{array}{l}{4^2} - 4m > 0\\0 + m > 0\\{3^2} - 4.3 + m > 0\\0 < \frac{4}{2} < 3\end{array} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{4 - m > 0}\\{m > 0}\\{m - 3 > 0}\\{0 < 2 < 3}\end{array} \Leftrightarrow 3 < m < 4} \right.} \right.\)
Vậy 3 < m < 4.
Câu 3
A. m ≥ f(1) – e
B. \(m > f\left( { - 1} \right) - \frac{1}{e}\)
C. \(m \ge f\left( { - 1} \right) - \frac{1}{e}\)
D. m > f(1) – e .
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. G = 1
B. \(G = \frac{{ - 4}}{5}\)
C. \(G = \frac{{ - 6}}{5}\)
D. G = –1.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. 665 280
B. 85 680
C. 119
D. 579 600.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập