Câu hỏi:

30/10/2023 1,389

Một túi đựng 24 viên vi giống hệt nhau chỉ khác màu, với 9 viên bi màu đỏ, 6 viên bi màu xanh, 4 viên bi màu vàng và 5 viên bi màu đen. Bạn Mai rút ngẫu nhiên một viên bi từ túi.

a) Có bao nhiêu kết quả có thể?

b) Chứng tỏ rằng các kết quả có thể không đồng khả năng. Tính xác suất để xảy ra mỗi kết quả có thể đó.

c) Tính xác suất để rút được viên bi màu đỏ hoặc màu vàng.

d) Tính xác suất để rút được viên bi không có màu đen.

Xem lời giải

Câu hỏi trong đề: Giải SBT Toán 8 KNTT Bài tập ôn tập cuối năm có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

Lời giải

a) Có 24 viên bi giống hệt nhau chỉ khác màu với bốn màu là: màu đỏ, màu xanh, màu vàng, màu đen. Do đó, có bốn kết quả có thể là: Rút được viên bi màu đỏ; Rút được viên bi màu xanh; Rút được viên bi màu vàng; Rút được viên bi màu đen.

b) Vì số lượng viên bi mỗi màu khác nhau nên các kết quả có thể không đồng khả năng.

Gọi A là biến cố “Rút được viên bi màu đỏ”. Do bạn Mai rút ngẫu nhiên 1 viên bi từ trong túi có 24 viên bi nên có 24 kết quả đồng khả năng.

Vì có 9 viên bi màu đỏ nên số kết quả thuận lợi của A là 9. Xác suất của biến cố A là: \(P\left( A \right) = \frac{9}{{24}} = \frac{3}{8}\).

Gọi B là biến cố: “Rút được viên bi màu xanh”. Vì có 6 viên bi màu xanh nên số kết quả thuận lợi của B là 6. Xác suất của biến cố B là: \(P\left( B \right) = \frac{6}{{24}} = \frac{1}{4}\).

Gọi C là biến cố: “Rút được viên bi màu vàng”. Vì có 4 viên bi màu vàng nên số kết quả thuận lợi của C là 4. Xác suất của biến cố C là: \(P\left( C \right) = \frac{4}{{24}} = \frac{1}{6}\).

Gọi D là biến cố: “Rút được viên bi màu đen”. Vì có 5 viên bi màu đen nên số kết quả thuận lợi của D là 5. Xác suất của biến cố D là: \(P\left( D \right) = \frac{5}{{24}}\).

c) Gọi E là biến cố: “Rút được viên bi màu đỏ hoặc màu vàng”. Vì có 9 viên bi màu đỏ và 4 viên bi vàng nên số kết quả thuận lợi của E là: 9 + 4 = 13.

Xác suất của biến cố E là: \(P\left( E \right) = \frac{{13}}{{24}}\).

d) Gọi F là biến cố: “Rút được viên bi không có màu đen”. Vì có 9 viên bi màu đỏ, 4 viên bi vàng, 6 viên bi màu xanh nên số kết quả thuận lợi của F là: 9 + 4 + 6 = 19. (Hoặc sử dụng do có 5 viên bi màu đen nên số viên bi không có màu đen là 24 – 5 = 19).

Xác suất của biến cố F là: \(P\left( F \right) = \frac{{19}}{{24}}\).

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là chân các đường vuông góc hạ từ H xuống AB, AC và M là trung điểm của BC. Chứng minh rằng:

a) EF = AH.

b) AM ⊥ EF.

Xem đáp án

Lời giải

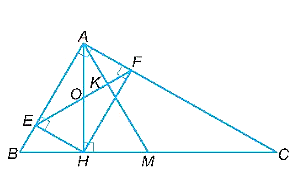
Media VietJack

a)Vì tam giác ABC vuông tại A nên \(\widehat {BAC} = 90^\circ \).

Vì E, F lần lượt là chân các đường vuông góc hạ từ H xuống AB, AC nên HE vuông góc với AB, HF vuông góc với AC.

Do đó, \(\widehat {HEB} = \widehat {HEA} = \widehat {HFA} = \widehat {HFC} = 90^\circ \).

Xét tứ giác AFHE có: \(\widehat {BAC} = \widehat {HEA} = \widehat {HFA} = 90^\circ \).

Do đó, tứ giác AFHE là hình chữ nhật.

Suy ra AH = FE (hai đường chéo bằng nhau).

b) Vì tứ giác AFHE là hình chữ nhật nên \(\widehat {FHE} = 90^\circ \).

Vì AM là đường trung tuyến trong tam giác ABC vuông tại A nên

AM = MB = MC = \(\frac{1}{2}BC\).

Tam giác AMB có AM = MB nên tam giác AMB cân tại M.

Do đó, \(\widehat {MAB} = \widehat B\).

Lại có \(\widehat B = \widehat {AHE}\,\,\,\,\,\left( { = 90^\circ - \widehat {HEB}} \right)\).

Nên \(\widehat {MAB} = \widehat {AHE}\) (1).

Gọi O là giao điểm của hai đường chéo FE và AH của hình chữ nhật AFHE.

Do đó, OH = OE = OF = OA.

Tam giác OAE có OA = OE nên tam giác OAE cân tại O.

Suy ra \(\widehat {OEA} = \widehat {OAE}\).

Mà AE song song với FH (do AFHE là hình chữ nhật) nên \(\widehat {OHF} = \widehat {OAE}\) (hai góc so le trong).

Do đó, \(\widehat {OEA} = \widehat {OHF}\) (2).

Lại có \(\widehat {OHF} + \widehat {OHE} = \widehat {FHE} = 90^\circ \) (3).

Từ (1), (2), (3) ta có: \[\widehat {MAB} + \widehat {OEA} = 90^\circ \].

Gọi K là giao điểm của AM và EF. Khi đó, \[\widehat {KAE} + \widehat {KEA} = 90^\circ \]. Suy ra \(\widehat {AKE} = 90^\circ \).

Vậy AM vuông góc với EF tại K.

Câu 2

Cho hàm số y = (3m + 1)x – 2m.

a) Tìm điều kiện của m để hàm số đã cho là hàm số bậc nhất.

b) Tìm m để đồ thị hàm số đã cho là đường thẳng song song với đường thẳng y = –2x + 5.

c) Với m tìm được ở câu b), hãy vẽ đồ thị của hàm số đã cho.

Xem đáp án

Lời giải

a) Hàm số y = (3m + 1)x – 2m là hàm số bậc nhất khi 3m + 1 ≠ 0, tức là m ≠ \(\frac{{ - 1}}{3}\).

b) Vì đồ thị hàm số đã cho là đường thẳng song song với đường thẳng y = –2x + 5 nên

3m + 1 = –2 và –2m ≠ 5.

Tức là m = –1 và m ≠ \(\frac{{ - 5}}{2}\). Suy ra m = – 1.

Vậy m = – 1.

c) Với m = –1, ta có y = –2x + 2.

Đồ thị hàm số y = –2x + 2 là đường thẳng đi qua hai điểm A(0; 2), B(1; 0) như hình dưới đây.

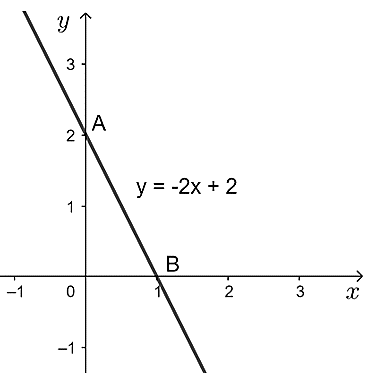
Media VietJack

Câu 3