Cho tam giác nhọn ABC có ba đường cao AM, BN, CQ cắt nhau tại H.
Đường thẳng QN cắt đường thẳng BC tại F. Chứng minh rằng FB . FC = FQ . FN.
Cho tam giác nhọn ABC có ba đường cao AM, BN, CQ cắt nhau tại H.
Đường thẳng QN cắt đường thẳng BC tại F. Chứng minh rằng FB . FC = FQ . FN.
Câu hỏi trong đề: Giải SBT Toán 8 CTST Bài tập cuối chương 8 có đáp án !!
Quảng cáo
Trả lời:
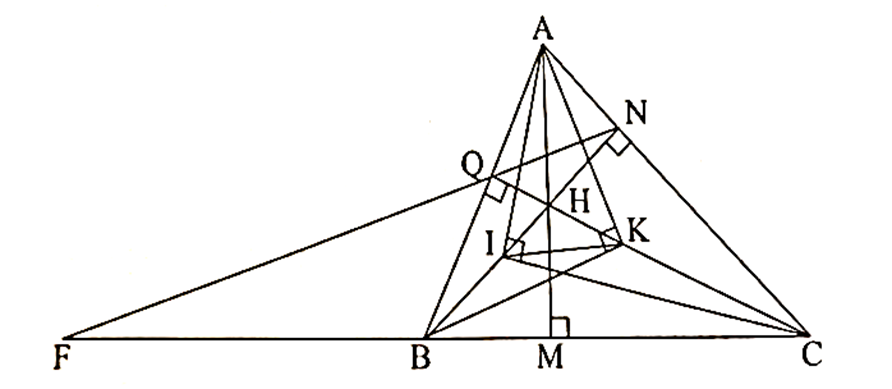
Xét ∆FQB và ∆FCN có
\[\widehat {CFN}\] chung; \[\widehat {FQB} = \widehat {FCN}\] \[\left( { = \widehat {AQN}} \right)\].
Do đó ∆FQB ᔕ ∆FCN (g.g).
Suy ra \[\frac{{FQ}}{{FC}} = \frac{{FB}}{{FN}}\]. Do đó FB . FC = FQ . FN (g.g).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: B
Nếu ∆ABC ᔕ ∆MNP theo tỉ số \[k = \frac{2}{3}\] thì tam giác MNP đồng dạng với tam giác ABC theo tỉ số \[\frac{1}{k} = \frac{3}{2}\].
Lời giải
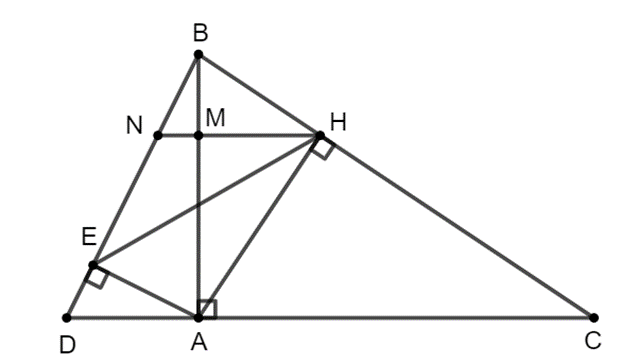
Xét ∆HBA vuông tại H và ∆HAC vuông tại H có
\[\widehat {BAH} = \widehat {ACH}\] (cùng phụ với \[\widehat {CAH}\]).
Do đó ∆HBA ᔕ ∆HAC (g.g).
Suy ra \[\frac{{AH}}{{CH}} = \frac{{BH}}{{AH}}\]. Do đó AH2 = BH . CH (đpcm).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.