✕

✨ Đăng kí VIP để truy cập không giới hạn. Đăng ký ngay

Câu hỏi:

29/11/2023 377

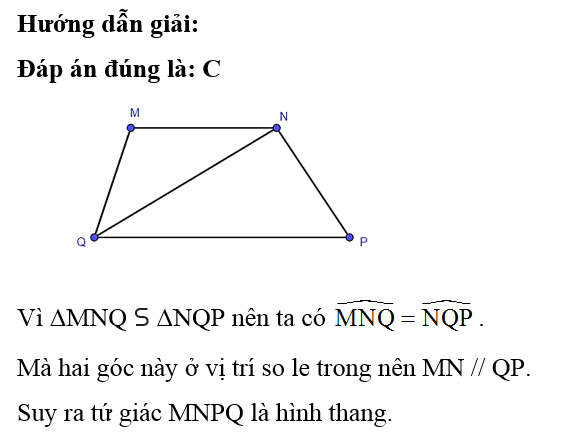
Cho tứ giác MNPQ. Đường chéo NQ chia tứ giác thành hai tam giác đồng dạng với nhau là ΔMNQ và ΔNQP. Khẳng định nào sau đây là đúng?

A. MNPQ là hình chữ nhật;

B. MNPQ là hình bình hành;

C. MNPQ là hình thang;

D. MNPQ là hình vuông.

Xem lời giải

Câu hỏi trong đề: 10 Bài tập Trường hợp đồng dạng đặc biệt của hai tam giác (có lời giải) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Cho tứ giác MNPQ. Đường chéo NQ chia tứ giác thành hai tam giác đồng dạng với nhau là ΔMNQ và ΔNQP. Khẳng định nào sau đây là đúng? (ảnh 1)

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hình vẽ sau biết MN // AB. Khẳng định nào sau đây là sai?

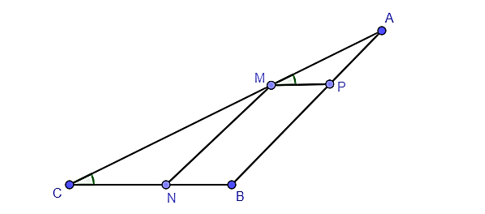
A. ΔAMP ᔕ ΔACB;

B. ΔMCN ᔕ ΔACB;

C. ΔAMP ᔕ ΔMCN;

D. Cả A, B, C đều sai.

Lời giải

Hướng dẫn giải:

Đáp án đúng là: D

Xét tam giác ABC, do MN // AB nên ΔMCN ᔕ ΔACB.

Lại có $\hat{AMP} = \hat{ACB}$ mà hai góc này ở vị trí đồng vị nên MP // CB.

Xét tam giác ABC, do MP // CB nên ΔAMP ᔕ ΔACB.

Vì ΔMCN ᔕ ΔACB, ΔAMP ᔕ ΔACB nên ΔAMP ᔕ ΔMCN.

Vậy D sai.

Câu 2

Cho tam giác ABC có M, N, P lần lượt là trung điểm các cạnh AB, AC, BC. Trong hình vẽ được có bao nhiêu cặp tam giác đồng dạng?

A. 4;

B. 6;

C. 8;

D. 10.

Lời giải

Hướng dẫn giải:

Đáp án đúng là: D

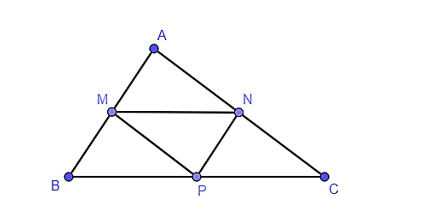
Cho tam giác ABC có M, N, P lần lượt là trung điểm các cạnh AB, AC, BC. Trong hình vẽ được có bao nhiêu cặp tam (ảnh 1)

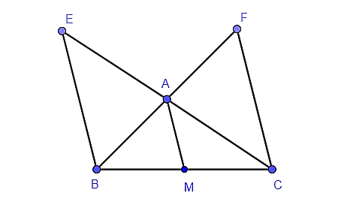
Vì M, N lần lượt là trung điểm của AB, AC.

Suy ra MN là đường trung bình của tam giác ABC nên MN // BC.

Vì M, P lần lượt là trung điểm của AB, BC.

Suy ra MP là đường trung bình của tam giác ABC nên MP // AC.

Vì N, P lần lượt là trung điểm của AC, BC.

Suy ra NP là đường trung bình của tam giác ABC nên NP // AB.

Xét tam giác ABC:

+ Do MN // BC nên ΔAMN ᔕ ΔABC.

+ Do MP // AC nên ΔMBP ᔕ ΔABC.

+ Do NP // AB nên ΔNPC ᔕ ΔABC.

Vì ΔAMN ᔕ ΔABC, ΔMBP ᔕ ΔABC, ΔNPC ᔕ ΔABC nên các tam giác AMN, MBP, NPC đôi một đồng dạng với nhau.

Xét hai tam giác AMN và PNM có:

AM = PN $= \frac{1}{2} AB$

MN: Cạnh chung

MP = AN $= \frac{1}{2} AC$

Suy ra ΔAMN = ΔPNM (c – c – c).

Do đó, ΔAMN ᔕ ΔPNM.

Từ đó suy ra 5 tam giác AMN, PNM, MBP, NPC, ABC đôi một đồng dạng với nhau.

Vậy có tất cả 10 cặp tam giác đồng dạng.

Câu 3

Cho tam giác ABC và các điểm M, N lần lượt trên các cạnh AB, AC sao cho MN // BC. Khẳng định nào sau đây là đúng?

A. $\frac{AM}{AB} = \frac{AN}{AC} = \frac{MN}{BC}$ ;

B. $\frac{AM}{AB} = \frac{AC}{AN} = \frac{MN}{BC}$ ;

C. $\frac{AB}{AM} = \frac{AC}{AN} = \frac{MN}{BC}$ ;

D.

\frac{AM}{AB} = \frac{AN}{AC} = \frac{BC}{MN}

.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho hình dưới đây, khi đó độ dài cạnh AC

A. 3;

B. $\frac{4}{3}$ ;

C. 12;

D.

\frac{16}{3}

.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho hình vẽ, biết BE // AM // CF. Khi đó $\frac{1}{BE} + \frac{1}{CF}$ bằng

A. $\frac{1}{AM}$ ;

B. $\frac{1}{B C}$ ;

C. $\frac{2}{AM}$ ;

D. $\frac{2}{B C}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho hình bình hành ABCD. Lấy E trên cạnh BC, tia DE cắt AB tại F. Khi đó tam giác FBE đồng dạng với tam giác nào dưới đây?

A. Tam giác FAD;

B. Tam giác DCE;

C. Cả A, B đều sai;

D. Cả A, B đều đúng.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Cho hình sau, hãy chỉ ra hai tam giác đồng dạng và tỉ số đồng dạng của hai tam giác đó.

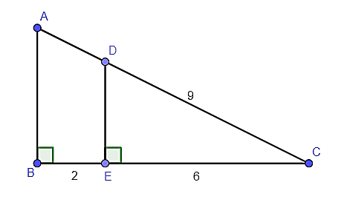
A. ΔCAB ᔕ ΔCDE với tỉ số đồng dạng $k = \frac{CA}{CD}$ ;

B. ΔABC ᔕ ΔDEC với tỉ số đồng dạng $k = \frac{AB}{DE}$ ;

C. ΔDEC ᔕ ΔBAC với tỉ số đồng dạng $k = \frac{BC}{DC}$ ;

D. ΔDEC ᔕ ΔBAC với tỉ số đồng dạng

k = \frac{DE}{BA}

.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Vietjack official store

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

🔥 Đề thi HOT:

Bạn vui lòng để lại thông tin để được
TƯ VẤN THÊM

Hoặc gọi Hotline tư vấn: 084 283 45 85
Email: vietjackteam@gmail.com

VietJack