✕

✨ Đăng kí VIP để truy cập không giới hạn. Đăng ký ngay

Câu hỏi:

11/07/2024 1,648

Chứng minh tồn tại vô hạn các số nguyên tố.

Xem lời giải

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Giả sử chỉ có hữu hạn các số nguyên tố là p₁; p₂; p₃; …; pn và giả sử p₁ < p₂ < p₃ < ... < p_n.

Xét tích A = p₁. p₂. p₃. …p_{n + 1}. Rõ ràng A > p_n nên A là hợp số, do đó A có ít nhất một ước nguyên tố p.

Khi đó p₁; p₂; p₃; …; pn là tất cả các số nguyên tố nên tồn tại I thuộc {1, 2, …, n} sao cho p = p_i.

Như vậy A chia hết cho p; p₁; p₂; p₃; …; pn chia hết cho p nên 1 chia hết cho p, mâu thuẫn.

Do đó, giả sử chỉ có hữu hạn số nguyên tố là sai.

Vậy có vô hạn các số nguyên tố.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho tam giác ABC. Các điểm M, N, P lần lượt là trung điểm của AB, AC, BC. Xác định hiệu $\vec{A M} - \vec{A N}, \vec{M N} - \vec{N C}, \vec{M N} - \vec{P N}, \vec{B P} - \vec{C P}$

Xem đáp án

Lời giải

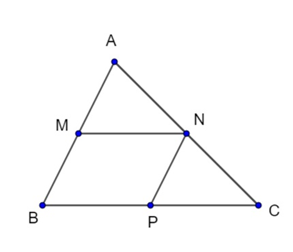
Cho tam giác ABC. Các điểm M, N, P lần lượt là trung điểm của AB, AC, BC. Xác định hiệu am - an, mn - nc , mn - pn, bp - cp (ảnh 1)

* $\vec{A M} - \vec{A N} = \vec{A M} + \vec{N A} = \vec{N M}$

N là trung điểm AC nên $\vec{A N} = \vec{N C}$

* $\vec{M N} - \vec{N C} = \vec{M N} - \vec{A N} = \vec{M N} + \vec{N A} = \vec{M A}$

Xét tam giác ABC có: M, N là trung điểm AB, AC nên MN là đường trung bình

Suy ra: MN // BC; $M N = \frac{1}{2} B C = B P = P C$

=> $\vec{M N} = \vec{P C}$

* $\vec{M N} - \vec{P N} = \vec{P C} - \vec{P N} = \vec{N C}$

* $\vec{B P} - \vec{C P} = \vec{B P} + \vec{P C} = \vec{B C}$

Câu 2

Tìm m để A giao B bằng rỗng biết A = [m; m + 1] và B = (-1; 3).

Xem đáp án

Lời giải

Để A ∩ B = ∅ thì:

[\begin{array}{l} m + 1 \leq - 1 \\ m \geq 3 \end{array} \Leftrightarrow [\begin{array}{l} m \leq - 2 \\ m \geq 3 \end{array}

Câu 3

Cho $\frac{a}{b + c} + \frac{b}{a + c} + \frac{c}{a + b} = 1$ . Chứng minh rằng $\frac{a^{2}}{b + c} + \frac{b^{2}}{a + c} + \frac{c^{2}}{a + b} = 0$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Tìm tất cả các giá trị của tham số m để đồ thị hàm số y = x³ + 2x² + (m − 3)x + m

có hai điểm cực trị và điểm M(9; −5) nằm trên đường thẳng đi qua hai điểm cực trị của đồ thị.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho hình chóp S.ABCD, đáy là hình bình hành ABCD. Gọi M, N lần lượt là trung điểm SA, CD. Chứng minh MN // (SBC).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Một cung lượng giác trên đường tròn định hướng có độ dài bằng một nửa bán kính. Số đo theo rađian của cung đó là?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

cho hình bình hành ABCD, đường chéo AC lớn hơn đường chéo BD, kẻ CH vuông góc với AD, CK vuông góc với AB.

a, Chứng minh tam giác BCK đồng dạng tam giác DCH.

b, Chứng minh tam giác CKH đồng dạng tam giác BCA.

c, Chứng minh HK = AC.sin $\hat{B A D}$

d, Tính diện tích của tứ giác AKCH nếu , AB = 4cm, AC = 5cm.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »