Một con tàu khởi hành từ đảo A, đi thẳng về hướng đông 10 km rồi đi thẳng tiếp 10 km về hướng nam thì tới đảo B (H.4.2). Nếu từ đảo A, tàu đi thẳng (không đổi hướng) tới đảo B, thì phải đi theo hướng nào và quãng đường phải dài bao nhiêu kilômét?

Xem lời giải

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

Ta có hình vẽ sau:

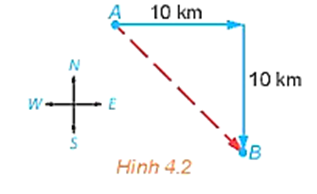
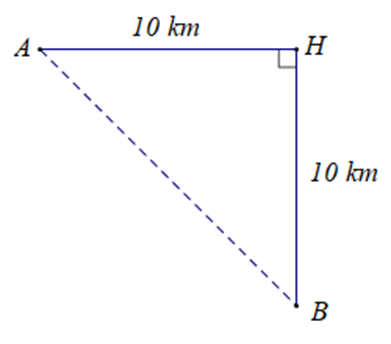
Một con tàu khởi hành từ đảo A, đi thẳng về hướng đông 10 km rồi đi thẳng tiếp 10 km về hướng nam thì tới đảo B (H.4.2). Nếu từ đảo A, tàu đi thẳng (ảnh 2)

Vì góc giữa hướng đông và hướng nam là bằng 90 độ nên $\hat{A H B} = 90 °$

do đó tam giác AHB vuông tại H.

Xét ΔAHB vuông tại H, áp dụng định lí Py – ta – go ta có: AB² = AH² + BH²

Thay số: AB² = 102 + 10 = 100 + 100 = 200

⇔ $A B = \sqrt{200} = 10 \sqrt{2} (k m)$

ΔAHB vuông tại H, có AH = BH = 10 km nên ΔAHB cân tại H

Suy ra: $\hat{H A B} = 45 °$

Do đó nếu đi từ đảo A, tàu đi thẳng (không đổi hướng) tới đảo B thì phải đi theo đường thẳng AB chính là hướng đông nam, tạo với hướng đông một góc 45°.

Vậy nếu từ đảo A, tàu đi thẳng (không đổi hướng) tới đảo B, thì phải đi theo hướng đông nam, tạo với hướng đông một góc 45° và đi quãng đường dài $10 \sqrt{2} k m .$

Đang tải chế độ Học...

Hot: 1000+ đề thi cuối kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho tam giác ABC. Các điểm M, N, P lần lượt là trung điểm của AB, AC, BC. Xác định hiệu $\vec{A M} - \vec{A N}, \vec{M N} - \vec{N C}, \vec{M N} - \vec{P N}, \vec{B P} - \vec{C P}$

Xem đáp án

Lời giải

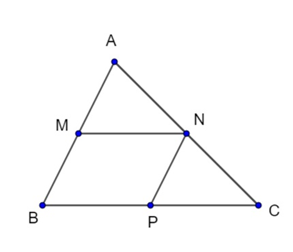
Cho tam giác ABC. Các điểm M, N, P lần lượt là trung điểm của AB, AC, BC. Xác định hiệu am - an, mn - nc , mn - pn, bp - cp (ảnh 1)

* $\vec{A M} - \vec{A N} = \vec{A M} + \vec{N A} = \vec{N M}$

N là trung điểm AC nên $\vec{A N} = \vec{N C}$

* $\vec{M N} - \vec{N C} = \vec{M N} - \vec{A N} = \vec{M N} + \vec{N A} = \vec{M A}$

Xét tam giác ABC có: M, N là trung điểm AB, AC nên MN là đường trung bình

Suy ra: MN // BC; $M N = \frac{1}{2} B C = B P = P C$

=> $\vec{M N} = \vec{P C}$

* $\vec{M N} - \vec{P N} = \vec{P C} - \vec{P N} = \vec{N C}$

* $\vec{B P} - \vec{C P} = \vec{B P} + \vec{P C} = \vec{B C}$

Câu 2

Tìm m để A giao B bằng rỗng biết A = [m; m + 1] và B = (-1; 3).

Xem đáp án

Lời giải

Để A ∩ B = ∅ thì:

[\begin{array}{l} m + 1 \leq - 1 \\ m \geq 3 \end{array} \Leftrightarrow [\begin{array}{l} m \leq - 2 \\ m \geq 3 \end{array}

Câu 3