Cho tam giác ABC, điểm D đối xứng vs A qua B, E đối xứng B qua C, F đối xứng C qua A Gọi G là giao điểm của đường trung tuyến AM. Trong tam giác ABC với trung tuyến DN của tam giác DEF Gọi I, K lần lượt là trung điểm của GA và GD.
1) Chứng minh tứ giác MNIK là hình bình hành.
2) Chứng minh tam giác ABC và tam giác DEF có cùng trọng tâm.
Cho tam giác ABC, điểm D đối xứng vs A qua B, E đối xứng B qua C, F đối xứng C qua A Gọi G là giao điểm của đường trung tuyến AM. Trong tam giác ABC với trung tuyến DN của tam giác DEF Gọi I, K lần lượt là trung điểm của GA và GD.
1) Chứng minh tứ giác MNIK là hình bình hành.
2) Chứng minh tam giác ABC và tam giác DEF có cùng trọng tâm.
Quảng cáo
Trả lời:
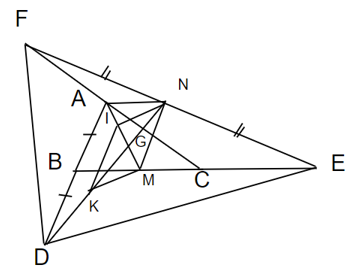
Nối A vs N
a) Xét tam giác CEF có: N là trung điểm của EF (gt) và A là trung điểm của FC (vì C đối xứng với F qua A)
⇒ AN là đường trung bình của tam giác CEF
⇒ AN//CE và
⇒ (vì BC = CE)
⇒ AN = BM(vì )
Xét tứ giác ANMB có: AN = MB (cmt) và AN//MB
(vì AN// CE; B, M, C, E thẳng hàng)
⇒ tứ giác ANMB là hình bình hành
⇒ MN // AB và AB = MN (1)
xét tam gíac AGD có: I là trung điểm của AG (gt) và K là trung điểm của DG (gt)
⇒ IK là đường trung bình của tam giác AGD
⇒ và IK //AD
Mà B là trung điểm của AD (vì A đx vs D qua B) ⇒ AB = BD = AD
⇒ IK = AB (= AD) (2)
Từ (1), (2) ⇒ IK = MN
Ta có: MN// AB (cmt); B thuộc AD ⇒ MN//AD
Xét tứ giác MNIK có: IK = MN (cmt) và IK // MN (cùng // AD)
⇒ tứ giác MNIK là hình bình hành (đpcm)
b) Do tứ giác MNIK là hình bình hành (câu a) mà G là giao điểm của IM và KN nên G là trung điểm của IM là KN
⇒ IG = MG và KG = NG
Mặt khác: I là trung điểm của AG (gt) ⇒ IG = AI ⇒ AI = IG = GM
K là trung điểm của DG (gt) ⇒ DK = KG ⇒ DK = KG = GN
xét tam giác ABC có: AM là đường trung tuyến và AI = IG = GM (cmt)
⇒ G là trọng tâm của tam giác ABC (*)
Xét tam giác DEF có: DN là đg trung tuyến (gt) và DK = KG = GN (cmt) ⇒ G là trọng tâm của tam giác DEF (**)
Từ (*), (**) ⇒ G vừa là trọng tâm của tam giác ABC vừa là trọng tâm của tam giác DEF
⇒ Tam giác ABC và tam giác DEF có cùng trọng tâm là G (đpcm).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
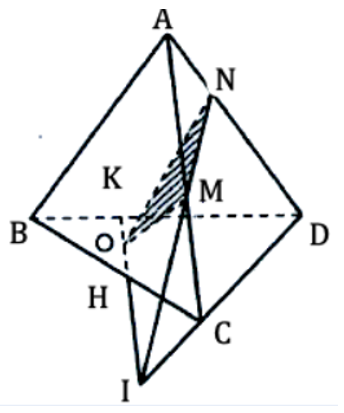
a) Trong mp(ACD) gọi I là giao điểm của NM và CD.
Khi đó OI = (OMN) ∩ (BCD)
b) Trong mp(BCD) gọi H, K là giao điểm OI với BC và BD
K, H ∈ OI nên K, H ∈ (OMN)
Vậy H = BC ∩ (OMN)
c) K, H ∈ OI nên K, H ∈ (OMN)
Nên K = BD ∩ (OMN).
Lời giải
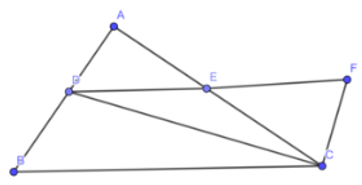
a) Xét tam giác AED và CEF có:
EA = EC
(đối đỉnh)
ED = EF
⇒ ∆AED = ∆CEF (c.g.c)
⇒ DA = CF
Mà DA = DB nên DB = CF
b) ∆AED = ∆CEF nên:
Suy ra: AB // CF
⇒ (so le trong)
Xét tam giác BDC và FCD có:
DC chung
BD = CF
⇒ ∆BDC = ∆FCD (c.g.c)
c) ∆BDC = ∆FCD nên
Suy ra: DE // BC (2 góc so le trong bằng nhau)
Lại có BC = DF = 2DE
Nên: .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.