Cho tam giác ABC nhọn có các đường cao AD, BE, CF cắt nhau tại H (Hình 61). Tìm trực tâm của các tam giác HAB, HBC, HCA.
Cho tam giác ABC nhọn có các đường cao AD, BE, CF cắt nhau tại H (Hình 61). Tìm trực tâm của các tam giác HAB, HBC, HCA.
Quảng cáo
Trả lời:
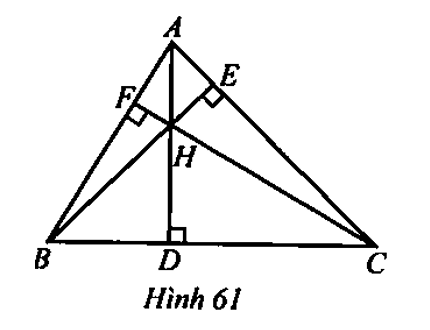
• Xét tam giác HAB có BD ⊥ AH, AE ⊥ BH, HF ⊥ AB và ba đường cao BD, AE, HF cắt nhau tại C.
Do đó C là trực tâm tam giác HAB.
• Xét tam giác HBC có HD ⊥ BC, BF ⊥ HC, CE ⊥ BH và ba đường cao HD, BF, CEcắt nhau tại A.
Do đó A là trực tâm tam giác HBC.
• Xét tam giác HCA có HE ⊥ AC, AF ⊥ HC, CD ⊥ AH và ba đường cao HE, AF, CD cắt nhau tại B.
Do đó B là trực tâm tam giác HCA.
Vậy trực tâm của các tam giác HAB, HBC, HCA tương ứng là C, A, B.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
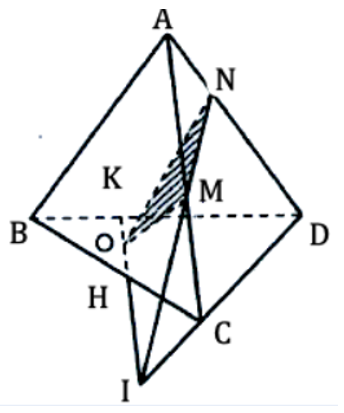
a) Trong mp(ACD) gọi I là giao điểm của NM và CD.
Khi đó OI = (OMN) ∩ (BCD)
b) Trong mp(BCD) gọi H, K là giao điểm OI với BC và BD
K, H ∈ OI nên K, H ∈ (OMN)
Vậy H = BC ∩ (OMN)
c) K, H ∈ OI nên K, H ∈ (OMN)
Nên K = BD ∩ (OMN).
Lời giải
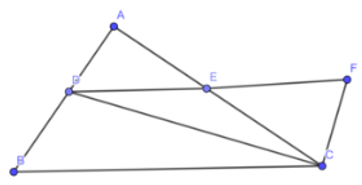
a) Xét tam giác AED và CEF có:
EA = EC
(đối đỉnh)
ED = EF
⇒ ∆AED = ∆CEF (c.g.c)
⇒ DA = CF
Mà DA = DB nên DB = CF
b) ∆AED = ∆CEF nên:
Suy ra: AB // CF
⇒ (so le trong)
Xét tam giác BDC và FCD có:
DC chung
BD = CF
⇒ ∆BDC = ∆FCD (c.g.c)
c) ∆BDC = ∆FCD nên
Suy ra: DE // BC (2 góc so le trong bằng nhau)
Lại có BC = DF = 2DE
Nên: .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.