Quảng cáo
Trả lời:
Ta có:
⇔ a8 + b8 + c8 ≥ a2b2c2(ab + bc + ca) (*)
Áp dụng bất đẳng thức AM-GM:
a8 + b8 ≥ 2a4b4
b8 + c8 ≥ 2b4c4
a8 + c8 ≥ 2a4c4
⇒ a8 + b8 + c8 ≥ a4b4 + b4c4 + c4a4
Tiếp tục áp dụng AM-GM:
a8 + b8 + a4b4 + c8 ≥
b8 + c8 + b4c4 + a8 ≥ 4b3c3a2
c8 + a8 + a4c4 + b8 ≥ 4c3a3b2
Cộng lại ta được:
3(a8 + b8 + c8) + (a4b4 + b4c4 + a4c4) ≥ 4a2b2c2(ab + bc + ca)
Mà a8 + b8 + c8 ≥ a4b4 + b4c4 + a4c4
Nên: 4(a8 + b8 + c8) ≥ 4a2b2c2(ab + bc + ca)
Hay a8 + b8 + c8 ≥ a2b2c2(ab + bc + ca)
Suy ra: (*) đúng
Vậy ta có điều phải chứng minh.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
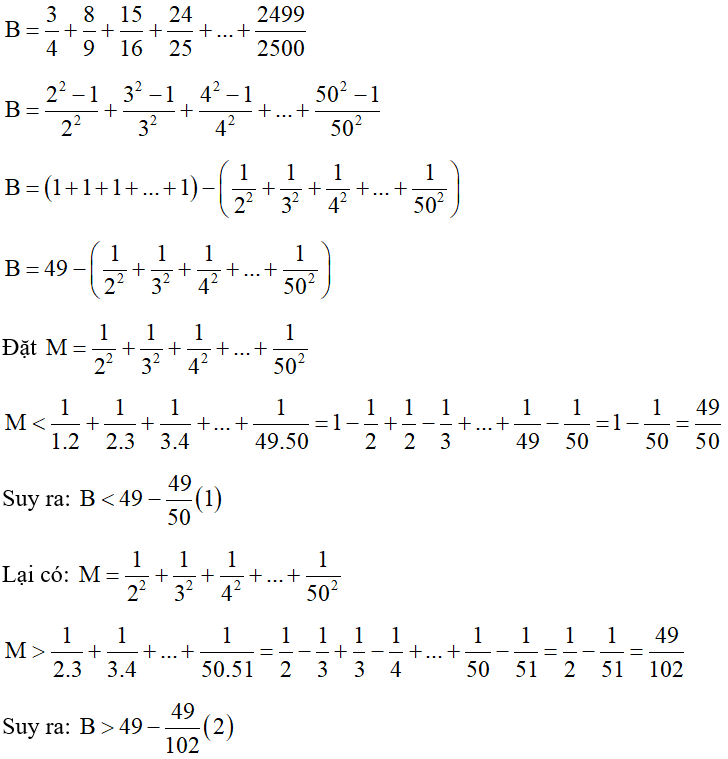
Từ (1) và (2) ta có:
⇒
Vậy B không phải là số nguyên.
Lời giải
A = x2 – 4x + 7
A = x2 – 4x + 4 + 3
A = (x – 2)2 + 3
Ta thấy (x – 2)2 ≥ 0 với mọi x nên (x – 2)2 + 3 ≥ 3 với mọi x
Hay A ≥ 3
Vậy GTNN của A = 3 khi x – 2 = 0 hay x = 2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.