Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình x4 − 4x2 – 4 + 2m = 0 có 4 nghiệm phân biệt.

Ta có: x4 − 4x2 – 4 + 2m = 0 ⇔ x4 – 4x2 – 4 = –2m (1) Số nghiệm của (1) là số giao điểm của đồ thị hàm số y = x4 – 4x2 – 4 với đường thẳng y = - 2m. Xét hàm số y = x4 – 4x2 – 4 Tập xác định: D = ℝ Ta có: y’ = 4x3 – 8x, y’ = 0 ⇔ x=0x=±2 Ta có bảng biến thiên: Dựa vào bảng biến thiên, để (1) có 4 nghiệm phân biệt thì: -8 < -2m < -4 hay 2 < m < 4 Vậy 2 < m < 4 thì phương trình x4 − 4x2 – 4 + 2m = 0 có 4 nghiệm phân biệt.

Câu hỏi:

12/07/2024 5,185

Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình

x⁴ − 4x² – 4 + 2m = 0 có 4 nghiệm phân biệt.

Xem lời giải

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Ta có: x⁴ − 4x² – 4 + 2m = 0

⇔ x⁴ – 4x² – 4 = –2m (1)

Số nghiệm của (1) là số giao điểm của đồ thị hàm số y = x⁴ – 4x² – 4 với đường thẳng y = - 2m.

Xét hàm số y = x⁴ – 4x² – 4

Tập xác định: D = ℝ

Ta có: y’ = 4x³ – 8x, y’ = 0 ⇔ $[\begin{array}{l} x = 0 \\ x = \pm \sqrt{2} \end{array}$

Ta có bảng biến thiên:

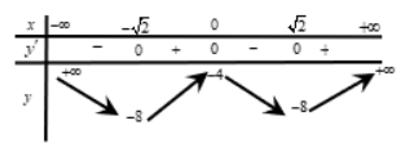
Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình x^4 − 4x^2 – 4 + 2m = 0 có 4 nghiệm phân biệt. (ảnh 1)

Dựa vào bảng biến thiên, để (1) có 4 nghiệm phân biệt thì:

-8 < -2m < -4 hay 2 < m < 4

Vậy 2 < m < 4 thì phương trình x⁴ − 4x² – 4 + 2m = 0 có 4 nghiệm phân biệt.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Tập hợp tất cả các giá trị thực của m để hàm số $y = \frac{x + 4}{x + m}$ đồng biến trên khoảng (–∞; –7) là:

A. [4; 7).

B. (4; 7).

C. (4; 7].

D. (4; +∞).

Xem đáp án

Lời giải

Đáp án đúng là: C

Tập xác định: D = ℝ\{–m}

Ta có: $y' = \frac{m - 4}{{(x + m)}^{2}}$

Hàm số đã cho đồng biến trên khoảng (–∞; –7) ⇔ y’ > 0 với mọi x ∈ (–∞; –7)

⇔ $\{\begin{cases} m - 4 > 0 \\ - m \notin (- \infty; - 7) \end{cases} \Leftrightarrow \{\begin{cases} m - 4 > 0 \\ - m \geq - 7 \end{cases} \Leftrightarrow 4 < m \leq 7$ .

Câu 2

Tìm một số có 3 chữ số, biết rằng chữ số hàng trăm gấp 2 lần chữ số hàng chục, chữ số hàng chục gấp 3 lần chữ số hàng đơn vị.

Xem đáp án

Lời giải

Gọi số có 3 chữ số cần tìm là $\bar{a b c} (a \neq 0; a, b, c < 10)$

Ta có: a = 2b; b = 3c

Suy ra: a = 2.3c = 6c

Mà a < 10 nên 6c < 10 ⇒ c < 2

Mặt khác c ≠ 0 để a ≠ 0

Vậy c = 1.

Khi đó a = 6c = 6

b = 3c = 3

Vậy số có 3 chữ số cần tìm là 631.

Câu 3